Оглавление:






Устойчивость движения. Прямой метод исследования
- Используя систему дифференциальных уравнений движения в виде первичной системы, мы изучаем устойчивость движения системы, где yk — обобщенные координаты или обобщенная скорость системы и является функцией времени. Если с-1 ф 24 является конкретным решением I системы, соответствующим начальным условиям данного упражнения . 3 3 L 3 10 .. .. 3 л Ло ЧРИ. Решение 2 определяет непертурбативное движение системы. Недоминирующее движение при незначительном изменении начальных условий решения системы изотоп называется устойчивым. 2 Перейдите к решению, которое почти совпадает с первым решением для того, насколько велико значение.
Такое непертурбативное упражнение называется также устойчивым упражнением малого размера. Кроме того, когда отклонение от возмущающего движения вследствие неограниченного увеличения времени стремится к нулю, такое возмущающее движение называется асимптотической устойчивостью. В некоторых технических вопросах недостаточно исследовать устойчивость малых движений.
Итак, для осуществления движения материальной точки в пло-скости необходимо и достаточно, чтобы начальная скорость точки и равнодействующая сил, приложенных к этой точке, лежали в одной плоскости. Людмила Фирмаль
Затем необходимо отбросить ограничения, накладываемые на отклонения начальных условий движения, которые возмущены от начальных условий невозмущенного движения. Непертурбативное движение системы называется асимптотической устойчивостью в большом масштабе, когда решение системы уравнений i, Начиная с определенного значения времени, немного отклоняется от решения 2, для начальных условий, отличных от 3. Отклонение начальных условий движения от условий, приведенных в Формуле 3, называется возмущением. Другие определения моторной стабильности possible.
В частности, во многих задачах современной техники важно обеспечить решение дифференциальных уравнений возмущений на конечных временных интервалах и малых отклонениях решения непертурбативных движений. При решении задачи об устойчивости движения в этой точке применяется прямой метод интегрирования дифференциальных уравнений возмущенного движения. Этот метод наиболее эффективен по своим результатам, но его применение ограничено небольшим числом возможных применений из-за математических трудностей, связанных с получением замкнутой формы решения.
При решении задачи строгости движения прямым методом интегрирования дифференциальных уравнений возмущающего движения рекомендуется применять только в случае необходимости. 1 Создать дифференциальные уравнения непертурбативного движения системы. 2 найти конкретное решение этой системы дифференциальных уравнений, соответствующее заданному исходному условию и определяющее незаметно движение системы. 3 Установите начальные условия для других ходов. 4 Создайте дифференциальное уравнение возмущенного движения. 5 найти решение путем интегрирования дифференциального уравнения возмущающего движения.
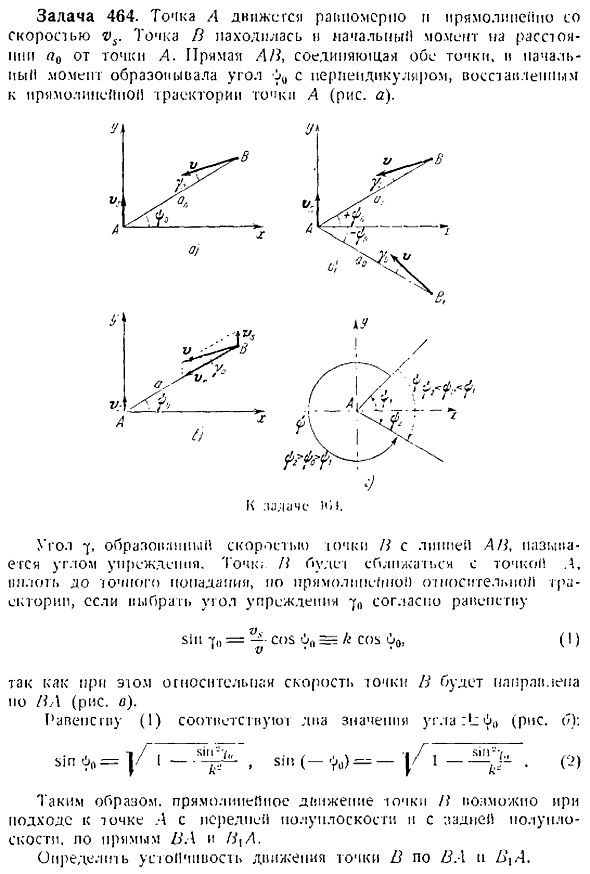
Сравнить решение дифференциального уравнения dw1 без возмущения и dw1 с возмущением для определения устойчивости движения без возмущения. Задача 464. Точка А движется равномерно и прямолинейно со скоростью y3. Точка 13 находилась в начальный момент расстояния l0 от точки a. Прямая линия a 3 соединяла обе точки, а начальный момент образовывал перпендикуляр, установленный на прямой путь точки a и угол y0 рисунок a. К задачам ИИ. Угол, образованный скоростью точки с линией а 3, 7, называется углом помещения.
При выборе угла опережения точки 13 будет приближаться к точке а по относительной траектории прямой линии до точного попадания Согласно уравнению 1pty —, потому что 0н г Кос ОО 1 В этом случае относительная скорость точки 13 обусловлена тем, что она направлена назад назад примерно по фигуре. Уравнение 1 соответствует 2 значениям угля kb0 рисунок b Я, З — — 1 −0 Следовательно, что такое линейное движение ючки Можно подойти к точке а из первой половины и второй половины, по линиям 13 А и у А. 13. X n a определяет устойчивость движения точки 13. Решение.
- Если рассматривать движение точки в как сложное движение, состоящее из переносного движения с точкой А и относительного движения относительно точки А, то вектор относительной скорости точки в направлен в точку а, подчиняясь уравнению 1 Рис. Наблюдатель, движущийся с точкой a, увидит точку b, движущуюся по линейной относительной траектории с постоянной скоростью h d. Это делает точку b непривлекательным движением. Предполагая, что угол опережения 7 не удовлетворяет уравнению i, точка Подумайте о движении возмущения. Если вы представите расстояние ab как a, вы найдете проекцию относительной скорости pa ab и проекцию на ось, перпендикулярную к ab.
В этих уравнениях показывает угол между осью x и прямой ab в данный момент времени. Уравнение 3 разделим уравнение 4 na и умножить обе части на. И sg, c bc-v 811 t При интегрировании этого уравнения с переменной Грина следует учитывать 3 частных случая. 1 81, с. 27 2 2 1p27 a 2 3 31p 7 l Первый случай малый угол опережения 51p 27 А 2. 5 при интеграции вы увидите следующее 1пСл 1ni i — k- −8111 7 06 4 4 i-5wr7 mp 6 1 С-В- 8i1 7 спящий b Где c-произвольная константа, а k — отношение скорости к k —. Он освобождается от логарифма и определяет c в соответствии с начальными условиями 1 0 a ac, fu.
Как было указано, тот же результат, по более громоздким способом можно получить с помощью формул, выведенных при решении предыдущей задачи. Людмила Фирмаль
Это уравнение относится к локусу точки b в возмущенном движении. 8 обратите внимание, что разные k дают разные заказы. Сон h r —Фр k 1 для 1 — Я к-1. 1 для k 1 при k 1 точка b обгоняет точку a под углом, определяемым уравнением 9 После этого Воля следовать из 7 исчезает. Если мы сравниваем значения 9 с учетом равенств 1 и 2, то угол угол г считается заключенным. Иными словами, в конце тренировки, появляется пункт Б по пути преувеличенные движения, который находится позади полуплоскость.
В результате, движение по относительной траектории АВ, который под углом относительно-оси Х, становится стабильный и большой. Каким бы ни было первое возмущение, точка b возвращается к линии ab с копией движения. Между тем, из равенства 4 10 В результате при прохождении прямой линии под углом определяется уравнение рисунок d Угол поворота линии ab меняет знак. Начальный угол меньше 0, а монотонно убывающий угол 6 в дальнейшем по ходу движения — это когда вкладка b выровнена по точке l. Если угол b0 больше b и меньше 62, то угол монотонно возрастает одинаково до, и та же точка b совпадает с точкой a рис. D.
В результате непертурбативное движение вдоль относительной орбиты ab, расположенной в первой полуплоскости, неустойчиво в малых полушариях. Независимо от того, насколько мал пирог, он отклоняется от траектории движения хора и щипка в первой полуплоскости, но при любом дальнейшем движении он отклоняется еще дальше от непертурбативной траектории и приближается к другой траектории пертурбативного движения во второй половине. 2-й случай k2. Интегрирование и определение уравнения 3 Любая константа ишегрования по начальным условиям и r 20 4 4 Найти уравнение относительной орбитали возмущенного движения, х я-И Л-Си 2 i—СО54 -, с-г- 122122-с.
Формула 10 в этом случае принимает вид Ф — i-СО О. 1 а 12 13 Поэтому угол поворота за напитка всегда положительный. Из Формулы 12 видно, что расстояние a исчезает как 4 — 0 из отрицательного side. So в этом случае обе орбиты изменчивы О движении рис. Г сливаются в 1 прямую ось, и углы 4 и 4 исчезают, respectively. In в этом случае необходимо определить устойчивость движения, а не прямую линию Ах, исходя из признаков возмущения.
Если первое отклонение приходится на 1-ю четверть, то точка в отклоняется дальше от прямой оси, а на минусовой стороне совпадает с точкой а на 4-6. Если начальное отклонение находится в 4-й четверти, точка b приближается к оси линии, а угол 40 стремится к zero. In в этом случае движения большие и стабильные.
Третий случай интегрируя уравнение o и определяя произвольную интегральную постоянную из начального условия a an, ffffor 0, находим уравнение относительной траектории движения возмущения 14 Из этой формулы видно, что по мере бесконечного увеличения угла а расстояние до точки А исчезает. Из уравнения 4 определите угол поворота линии 9 51n 7-a cos 4, 15 Оттуда y новая скорость не меняет знака. Символ соответствует символу mp y. Таким образом, траектория возмущения точки является point. 4. It это спираль, чтобы пройти через нее.
Смотрите также:
Предмет теоретическая механика

