Оглавление:




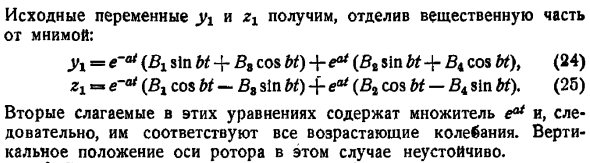

Устойчивость движения при наличии гироскопических сил
- Неустойчивая система может быть стабилизирована в первом приближении введением силы гироскопа только тогда, когда число неустойчивых степеней свободы четно. Эта теорема была доказана Кельвином. Стабилизация движения с помощью гироскопа возможна только в консервативной системе. Диссипативная сила действует достаточно долго, независимо от того, насколько она мала, чтобы разрушить стабильность, созданную силой гироскопа. Таким образом, стабильность, создаваемая силой гироскопа, называется временной, в то время как стабильность консервативной системы- долгосрочной.
Поэтому диссипативная сила увеличивает устойчивость движения под действием только силы сохранения и разрушает устойчивость, если устойчивость достигается добавлением гироскопа. если вадам решает изучить устойчивость движения под действием гироскопической силы, то рекомендуется следующий комплекс действий 1 определить число степеней свободы системы и выбрать обобщенные координаты. 2 Найти неупакованное движение системы.
Решить предыдущую задачу в предположении, что в начальный момент клин перемещался направо со скоростью тщ, а груз А находился в относительном покое. Людмила Фирмаль
Получить малые отклонения начальных условий движения и построить дифференциальные уравнения возмущающего движения с использованием уравнения Лагранжа или теоремы общей динамики.
Предположим, что обобщенные координаты и обобщенная скорость возмущения различны по величине непертурбативного движения и по меньшей величине 1-го порядка, линеаризуем дифференциальное уравнение, отбрасываем меньшие члены 2-го порядка или выше и вычитаем соответствующее уравнение непертурбативного движения из дифференциального уравнения возмущенного движения 5 исследование устойчивости системы в первом приближении путем прямого интегрирования дифференциальных уравнений Применение критерия фульвица к возмущениям или вариациям дифференциальных уравнений.
Задание 18.52. Ротор с массой Q вращается с постоянной угловой скоростью вокруг оси симметрии, совпадающей с неподвижной вертикальной осью X. точка O, центр сферической опоры Ротора, неподвижна. Центр тяжести Ротора C находится на высоте OS .Расстояние OAt l буква L1 обозначает самую нижнюю точку Ротора. Момент инерции ротора относительно оси симметрии равен а, а момент инерции относительно оси, перпендикулярной оси симметрии Ротора через точку О равен В. Исследовать устойчивость вертикального положения вала ротора. Ротор представляет собой систему с 2 степенями свободы. Давайте выберем координату ых На полюсе Ротора в качестве генерала coordinate.
- To составьте дифференциальное уравнение движения, примените теорему к изменению главных моментов импульса относительно неподвижной оси y, Z. Используя формулу в 9 2 этой главы, вы определяете главные моменты импульса для неподвижных осей. Л т бр — — — — о л. 1 Вводя в эти уравнения значения углов и y Мы получаем БР — АА С Р 3 ВЛ Аа а 1.И затем Косые члены симметрии — A opi и Ax x соответствуют силе гироскопа. Вводя комплексные переменные, мы находим решения системы однородных линейных уравнений с постоянными коэффициентами 5 Если вы умножите уравнение 4 на 1 и добавите его к уравнению 3 VK 1Apk-Q jX 0. 6 Создайте характеристическое уравнение БС СМВ-М, 0. 7 Определите корни этого уравнения.
Если условия выполнены A e 2 4BQZ1, 10. В таком случае корень-это значение чисто мнимой краткости, записанное в форме, и С1 З й, 11 Куда Б-А я — НЖ-4BQli 12 1 2В К-АА В АВ-4BQI, 13 2 2В Настоящий numbers. In в этом случае уравнение решение 6J 14 Где Di и Dt — любая комплексная константа вида Bj IBS, Dt Bt lBa. Уравнение 14 имеет вид Х Би Зса потому кДж з грех кит ВХ ПБ Дж кДж, потому что 1 грех кДж. 15 Далее находим начальные переменные yi и zit, которые разделяют действительную и мнимую части уравнения 15.
Вычислим проекцию на ось х главного вектора количеств движения системы в рассматриваемый момент времени. Людмила Фирмаль
В этих уравнениях B1, B2, B8 и B4 являются любыми константами интегрирования, определенными из начальных данных Z 0, y10,Jlo, Zi0, 2lt. Поскольку yy и zt являются линейными функциями Косинуса и синуса, нижний конец координатного Ротора не растет со временем. Таким образом, при выполнении условия 10 точка Yes совершает циклическое движение при условии, что Aj является допустимым, состоящее из 4 гармонических колебаний.
Следовательно, угловая скорость ротора 18 10, вертикальное положение оси ротора стабильно, несмотря на то, что центр тяжести занимает самое высокое положение, а равновесие того же невращающегося стержня неустойчиво. Мощность гироскопа стабилизирует неустойчивую консервативную систему. Давайте рассмотрим этот случай дальше Да.
Корни характеристического уравнения 7 являются комплексными числами вида 1 -а ЗБ, СД а ЗБ V4BQZ, −4 а 2В 0 20 21 В этом случае общее решение уравнения 6 имеет вид 22 Здесь, как и в первом случае, 1 B1 ZB D1 5J ZB4.Таким образом, это выражение замены 22 принимает вид Х РЖ zba успешно э э потому что БТ з грех БТ Б МБ е потому что БТ л грех БТ 23 Получим начальные переменные yi и gy, отделив действительную часть от мнимой. Джи е 0 ВХ грех Ш Б, потому что БТ еаз БТ грех БТ Б потому что БТ, 24 На ZX e a Би потому что БТ-В8 грех БТ БТ, потому что БТ-Би греха БТ. 26 2-й член этих уравнений включает коэффициенты e0, в результате чего они соответствуют колебаниям, которые продолжают увеличиваться.
Смотрите также:
Предмет теоретическая механика
| Устойчивость движения. Исследование по общему решению | Второй метод Ляпунова |
| Устойчивость движения по первому приближению | Преобразование Лапласа |

