Оглавление:






Устойчивость движения. Исследование по общему решению
- Для исследования устойчивости движения массовой системы запишите дифференциальное уравнение движения в виде линейной системы Л, 0С-1.2.2. Где Y-обобщенная координата и обобщенная скорость системы и является функцией времени t. Функциональная система л-А0. Пленки la0. Л О2 является ли конкретное решение в системе 1, которое соответствует начальным условиям данного движения ЛЛ ЛЛ ПР. Далее, решение 2 определяет движение системы без возмущений. Если при незначительном изменении начальных условий решение системы 2 переходит к решению, почти не отличающемуся от начального решения любого большого вычисления t, то беспрепятственное движение системы называется устойчивым.
Такое движение без возмущений называется также устойчивым движением малых движений. Более того, если отклонение от непертурбативного движения вследствие неограниченного увеличения времени стремится к нулю, то такое непертурбативное движение называется асимптотической устойчивостью. В некоторых технических вопросах недостаточно исследовать устойчивость малых движений. Затем необходимо отбросить ограничения, накладываемые на отклонения начальных условий движения, которые возмущены от начальных условий невозмущенного движения.
Определить импульс равнодействующей этой системы сил при перемещении материальной точки по дуге четверти окружности из точки А в точку В. Людмила Фирмаль
Для начальных условий, отличных от 3, если решение системы уравнений 1, начиная с определенного значения времени, отклоняется от решения 2 на величину, меньшую заданного значения, то беспрепятственное движение системы в целом называется асимптотической устойчивостью. Отклонение начального условия движения от заданного в уравнении 3 называется возмущением. Другие определения моторной стабильности possible. In в частности, во многих задачах новейшей техники важно обеспечить решение дифференциальных уравнений возмущений на конечных временных интервалах и малые отклонения решений непертурбативных движений.
При решении задачи об устойчивости движения в этой точке применяется прямой метод интегрирования дифференциальных уравнений возмущенного движения. Этот метод наиболее эффективен по своим результатам, но его применение ограничено небольшим числом возможных применений из-за математических трудностей, связанных с получением замкнутого решения. Если вы хотите решить проблему устойчивости движения путем интегрирования дифференциальных уравнений возмущений, рекомендуется следующая процедура 1.
Создайте дифференциальное уравнение для непертурбативного движения системы 2 найти конкретное решение для этой системы дифференциальных уравнений соответствующее заданному исходному условию и определяющее непертурбативное движение системы 3 Установите начальные условия для других упражнений 4 Создайте дифференциальное уравнение для возмущенного движения интегрируя дифференциальные уравнения движения возмущения B, мы находим их решения 6 сравните решение дифференциальных уравнений движения без возмущения и движения с возмущением для определения устойчивости движения без возмущения.
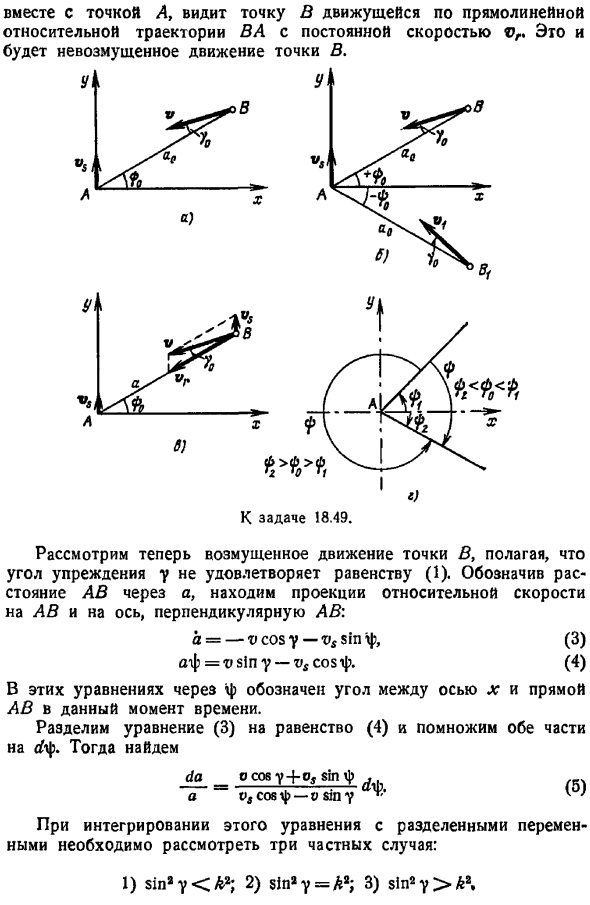
Задача 18.49. Точка А движется равномерно и прямолинейно со скоростью v5.Точка B находилась в начальный момент расстояния A0 от точки A. At в начальный момент прямая линия AB, соединяющая обе точки, образовала угол 0, который был выровнен перпендикулярно прямой траектории точки A на рисунке 1. один. Угол y0, образованный скоростью точки B и линии AB, называется прямым углом. Если угол y0 выбран в соответствии с уравнением, точка B приближается к точке A до тех пор, пока она не ударится точно по относительной траектории линии. sinу0cosф0Asovfo, я В этом случае, поскольку относительная скорость точки B направлена вдоль VA. с.
Уравнение 1 соответствует 2 значениям угла 0 на рисунке 2. z1pfvsln-ф0-2 б Поэтому линейное движение точки B возможно при приближении к точке A от передней полуповерхности и задней полуповерхности вдоль прямых BA и BHA. Определяет стабильность движения точки ва и бюстгальтера. Решение. Если рассматривать движение точки B как сложное движение, состоящее из пропорционального движения с точкой A и относительного движения с точкой A, то вектор относительной скорости точки B является точкой c фигуры, если соблюдается уравнение 1.Перемещение наблюдателя Вместе с точкой A убедитесь, что точка B движется по линейной относительной траектории VA с постоянной скоростью Vr.
- Это будет движение точки в без возмущений. Рассмотрим возмущающее движение точки B, предполагая, что прямой угол y не удовлетворяет уравнению 1. Если вы представите расстояние AB как a, вы найдете проекцию относительной скорости на оси, перпендикулярной AB и AB. В уютном-против sinф, 3 aiptsiny-cosip. Четыре В этих уравнениях показывает угол между осью x и прямой AB в данный момент времени. Разделите уравнение 3 на уравнение 4 и умножьте обе стороны на. А потом мы это выясним. Да И о, совф-о, на Пять При интегрировании этого уравнения с разделенной переменной необходимо учитывать 3 частных случая. 1 грех, грехи, 2 в,3 грехи в А. Первый случай-это малый прямой угол sin в A.
Если вы интегрируете 5 Шесть Где C-произвольная постоянная, а A-отношение скорости k vsv. Освободившись от логарифма и определив C начальным условием Z 0, получим a0,. Г-sinoscos22-sinsinsinфо Л-AvtusovfK-Шайни ФПЗ остановиться-Asovf 1-1П г грех г-Фе потока фр пребывании Ac0SijoJstay-Иосифа Семь Это уравнение относительной траектории точки B в возмущенном движении. обратите внимание, что K отличается, и показатель степени отличается — Ссы. Один Один Один На трассе А1 А1, А1.
Задачи на применение теоремы об изменении количества движения материальной точки следует решать в следующей последовательности: 1) изобразить на рисунке все силы, приложенные к материальной точке, т. Людмила Фирмаль
Восемь Для 1, точка B обгоняет точки А на угол определяется уравнением — ТЦФ. Затем 9 продолжается от 7.Если сравнить значения с равенством I и 2 в уравнении 9, то угол опережающего угла y — 0 равен concluded. In другими словами, в конце движения точка B выходит на орбиту непертурбативного движения, которое находится в конце plane. As в результате движение по относительной траектории AB под углом- 0 относительно оси x в значительной степени устойчиво. Независимо от начального разлома res, точка B в конце движения возвращается к линии AB. С другой стороны, из уравнения 4 Ага. Таким образом, при прохождении через прямую линию угла, определяемого уравнением на Рис. 1, г 11.
Угол поворота линии AB изменяет отметку. Если начальный угол меньше и больше, то при совпадении точки B с точкой A во время движения угол монотонно уменьшается до. Если угол 0 больше 1, но меньше 3, то угол монотонно возрастает до во время движения, при этом точка B снова совпадает с точкой A на Рис.1. d. As в результате непертурбативное движение вдоль относительной орбиты АВ, расположенной в первой полуплоскости, неустойчиво на малой полуплоскости.
Как бы ни было мало отклонение точки от траектории непертурбационного движения в первой полуплоскости, при дальнейшем движении она приближается к другой прямой траектории непертурбационного движения во второй полуплоскости, более удаленной от непертурбативной траектории. 2-й случай-sin2y A. Если проинтегрировать уравнение 5 и определить произвольную интегральную постоянную относительно начальных условий t0, то получим a0, 0 и найдем уравнение относительных орбит возмущенного движения. В этом случае уравнение 10 принимает вид Ф 1-софф. 13 в результате угол поворота линии VA всегда положительный.
Из уравнения 12, поскольку расстояние a исключается при 0 на отрицательной стороне, в этом случае обе траектории r непертурбативного движения на рисунке 1 сливаются в 1 прямую ось, а углы qx и qz исчезают, respectively. In в этом случае необходимо определить устойчивость движения вдоль прямой оси, исходя из признаков возмущения. Если начальное отклонение находится в 1-й четверти, то точка B находится дальше от прямой оси, а на отрицательной стороне совпадает с точкой A с 0.Если начальное отклонение находится в 4-й четверти, то точка B приближается к оси прямой, а угол 0 стремится к zero. In в этом случае движения большие и стабильные. 3-й случай-это грех.
Интегрировать уравнение 5 для определения начальной постоянное Условие a ao, f fr PRINFECT относительные уравнения Расширенная траектория движения Шабаш y-Lsovf IL m, r Y aijit-r-и из этого уравнения, если угол не ограничен, расстояние до точки A исчезнет. Из уравнения 4 угол поворота прямой скорости ф — siny-6 cosф, 15 Поэтому угловая скорость знака не меняет. Его признаки совпадают с признаками греха. Итак, траектория возмущения точки B-это спираль, проходящая через точку A.
Смотрите также:
Предмет теоретическая механика

