Оглавление:

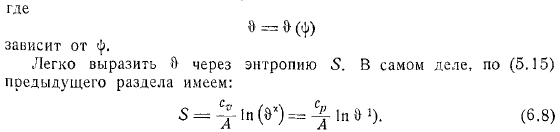



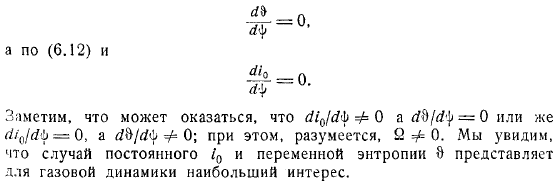

Установившиеся движения. Плоская задача. Функции
Точно так же во всех плоскостях, параллельных плоскости, рассмотрим установившееся движение газа, который в дальнейшем генерируется таким образом. Представляет решение задач по гидромеханике уравнения Эйлера в виде ОЗУ. Уравнение неразрывности имеет вид.
И условия теплоизоляции. Это уравнение позволяет сделать вывод, что существует функция потока, такая как. Между тем, наряду с рационализацией вы можете.
- Оставьте это уравнение, потому что оно получается без кучи, уравнение. Суть сильных разрывов теоремы Цемплена уравнения линии потока (последняя, благодаря постоянству, совпадает с локусом частицы жидкости и не изменяется в течение всего движения).
- Если вы умножите и вычитаете первый и второй элементы, это будет выглядеть так.
Но если это так, позвольте мне подумать о соотношении. Людмила Фирмаль
Поэтому мы приходим к выводу, что. Это зависит от. Это легко выразить в. Факт, в предыдущем разделе вы можете.
Теперь прибавим путем умножения на полученное уравнение, которое ранее было заменено формулой. С тех пор. И как результат, ведь он получается после простого преобразования.
- Это означает, что расположение только функция. Чтобы уточнить физический смысл, следует отметить, что есть кинетическая энергия разрыва в плоской задаче на единицу массы, и есть»калорийность» (обозначение приемлемо), поэтому если нет скорости, то есть калорийность.
- Значение — это температура.
Точка, в которой скорость падает до нуля. Это уравнение — не что иное, как уравнение Бернулли. Из уравнения мы получили только отношение. Отношение представляет собой вихри, и если они являются постоянными значениями (независимыми), это указывает на то, что движение без вихрей и наоборот-если движение без вихрей, вообще говоря, они.
На практике, например, вставьте его из уравнения Бернулли. Людмила Фирмаль
После сокращения, это выглядит так. Или, от и (зависит от носителя), наконец, в результате вы можете написать.
Выражение указывает, что, если они являются константами. Давайте сделаем наоборот. И если это, следовательно, функция. Этот случай не важен. Или в концентрических или параллельных прямых линиях, движения с линией потока соответствуют.
В общих чертах, если да. Или обратите внимание, что это может получиться; конечно, в то же время. Если энтропия постоянна и переменна, то видно, что она наиболее интересна для газовой динамики .

