Оглавление:




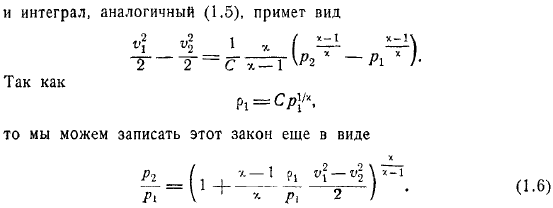


Установившееся движение
Дифференциальные уравнения гидромеханики движения идеальной жидкости допускают интегралы, аналогичные интегралу живой силы, в двух простейших случаях движения жидкости установившегося и безвихревого. Рассмотрим случай установившегося движения. В этом случае режим движения в каждой точке, занятой жидкостью, не изменяется с течением времени, и поле скоростей, поле вихрей, ноле гидродинамических давлений, поле массовых сил суть поля постоянные, или стационарные.
Линии тока при установившемся движении совпадают с траекториями жидких частиц. Умножая скалярно основное уравнение устойчивости равновесия движения на элементарное перемещение жидкой частицы вдоль линии тока, получаем. Так как при установившемся движении, то выражение является полным дифференциалом и можно написать. Последнее уравнение выражает собой не что иное, как закон живой силы для жидкой частицы. Это уравнение может быть без труда проинтегрировано при соблюдении двух условий если массовые силы имеют потенциал, который мы теперь обозначим через, так что, если жидкость баротропна.
В таком случае имеем где и все дифференциалы взяты при перемещении вдоль некоторой линии тока, или, иначе куда получаем так называемый интеграл. Где г есть величина, сохраняющая постоянное значение на данной линии тока, но, вообще говоря, изменяющаяся при переходе от одной безвихревого движение линии к другой. Если массовые силы суть силы тяжести, то, направив ось вертикально вверх, имеем, и интеграл Бернулли принимает вид. В уравнении первое слагаемое выражает высоту рассматриваемой жидкой частицы в данной трубке тока над некоторой горизонтальной плоскостью и называется геометрической высотой.
Во всех указанных разделах движение жидкости рассматривается как установившееся, так и неустановившееся (нестационарное). Людмила Фирмаль
Второе слагаемое выражает высоту, на которую могла бы подняться в пустоте материальная точка, брошенная вертикально вверх с начальной скоростью это слагаемое называется скоростной высотой. Наконец, третье слагаемое выражает высоту, которую должен бы иметь покоящийся столб жидкости, чтобы получить давление у основания столба это слагаемое называется пьезометрической высотой.
Таким образом, интеграл Бернулли выражает, что при установившемся, движении несжимаемой жидкости сумма геометрической, скоростной и пьезометрической высот остается неизменной для частиц одной и той же трубки тока, что может быть еще записано так или, если, в частности, геометрическая высота вдоль линий тока не меняется, то из баротропных случаев остановимся на изотермических и изоэнтропических движениях см. главы.
В изотермическом движении и интеграл Бернулли. примет вид по-прежнему в качестве сил берем силу тяжести. Для движений адиабатических и интеграл, аналогичный, примет вид. Так как мы можем записать этот закон еще в виде. Для воздуха можно считать. Если и не слишком велики, то как легко видеть, влияние сжимаемости будет незначительным. В самом деле, пусть, например, скорость имеет порядок. Тогда получим. Но тогда в разложении правой части мы можем ограничиться первыми двумя членами и вновь получим уравнение.
Основные разделы теоретической гидравлики: гидростатика; гидродинамика; кинематическая гидравлика. Людмила Фирмаль

