Оглавление:
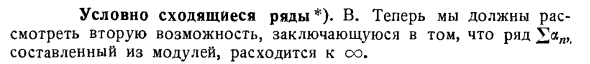

Условно сходящиеся ряды
- Ряд условной сходимости *). Б. Далее нам нужно рассмотреть вторую возможность, то есть возможность расхождения ряда модулей в ω. Определение сходится, но расходится> Первый ряд называется условной сходимостью. Во-первых, отметим, что если £ un условно сходится, оба ряда §191 £ vnt Tiwn будут переходить в oo. Это включает в себя сходимость £ (i / n-f-wn) или £ an, поэтому вы не можете сходить оба. И если один из них сходится, например, а другой расходится, N N N 2un = Zvn-2wn (1) ООО
Подобно Af-vco, £ un будет расходиться, что противоречит ожидаемой конвергенции £ un. Людмила Фирмаль
| Абсолютно сходящиеся ряды | Признаки сходимости условно сходящихся рядов |
| Обобщение теоремы Дирихле на абсолютно сходящиеся ряды | Знакочередующиеся ряды |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- В результате оба ряда расходятся с £ vn. От до В уравнении (1) ясно, что сумма ряда условной сходимости является пределом разности между двумя функциями, и каждая имеет тенденцию быть бесконечной, такой как η-> ω. Ряд условной сходимости также является свойством ряда с положительным членом (см. Пример XXX.18) и всех рядов абсолютной сходимости, где все ряды являются частью его членов (например, LXXVII.5 Также понятно, что вы больше не владеете) сходятся.
В любом случае, приведенное в § 192 доказательство здесь совершенно неуместно. Вскоре мы видим, что наше предположение действительно верно, т. Е. Теорема Дирихле не может быть расширена до ряда условной сходимости.
Кроме того, представляется весьма вероятным, что ряд условной сходимости не обладает свойством, которое составляет описание теоремы Дирихле. Людмила Фирмаль

