Оглавление:


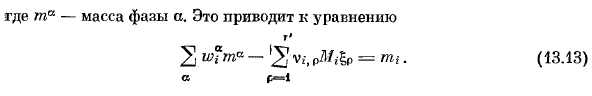

Условия замкнутости
- Условие закрытия В предыдущем параграфе мы рассмотрели условия, управляющие централизованными переменными. Правила фазы связаны с физико-химическими состояниями фаз, присутствующих в системе, и характеризуются интенсивными переменными величинами.
Если происходит процесс переноса вещества в систему или из системы, а также в замкнутую или замкнутую систему. Тогда необходимо отказаться от этого ограничения и перейти к полному учету состояния системы через интенсивное и экстенсивное variables.
Таким образом, правила фазы могут применяться к обеим открытым системам. Людмила Фирмаль
To для этого необходимо изучить замкнутую систему и выяснить количество переменных, которым необходимо придать определенное фиксированное значение, чтобы полностью определить равновесное состояние системы, то есть определить интенсивные и широкие переменные, характеризующие каждую фазу. Рассмотрим замкнутую систему, включающую компоненты и фазы рН. в замкнутой системе, в которой может происходить независимая реакция, увеличение числа молей компонента i во всей системе определяется по формуле (1.64′). г’ ДНР = 2 в», prfgp. (13) р = я Здесь сумма распространяется на все реакции, за исключением тех, которые уменьшаются просто от одной фазы к переходу вещества из одной Фазы в другую.
Конечно, вы не можете влиять на общее количество этого вещества в системе. Начальное число молей различных компонентов равно n …, t-равная ps°в 0, степень полноты реакции составляет Это начальное состояние(т. е.| i°= 0,…если, b = 0) измеряется относительно, (13.9) является tegrarate, ведущий к г’ U = 2 в, -, пип(я = 1,…, с.) (13.10) р = я I к значению 1, 2,…учитывая, что s выводится из уравнения, определяющего конечное состояние замкнутой системы.
- Умножением Mi (13.10)является молекулярная масса компонента£, и эти условия можно записать в виде: г’ Показатель= м -} — с. В.», pMfo,(13.10 ’) р = я Где Т-общая масса компонентов в системе. С тех пор Щ-S-S Но、 В условиях разделения можно ввести общее количество молей в каждой фазе. (13.10)в этом случае форма является г’ 2 2: в, -, п | п =. (и3.Ил) И Р = 1 Богатая масса каждой фазы(13.10 ’) Но… М = М-7(13.12) В 4 ′ Где ta-масса фазы a. это приводит к уравнению г’ 2-2 в *. Л-СП =•(13.13) Кондитерские изделия
Эти уравнения называются условиями замыкания. Людмила Фирмаль
Смотрите также:
Решение задач по термодинамике
| Энтропия идеального газа. | Теорема Дюгема |
| Энтропия и закон соответственных состояний. | Выбор независимых переменных |

