Оглавление:
Условия равновесия системы твердых тел
При определении условий равновесия системы твердых тел, находящихся во взаимодействии, задача о равновесии может быть разрешена для каждого тела в отдельности. Силы реакции (взаимодействия), возникающие в точках соприкосновения, удовлетворяют третьему закону Ньютона. В соответствии с этим мы обязаны принять условие, что действие одного тела на другое равно и противоположно по направлению действию этого другого тела на первое.
Если при решении задачи о равновесии выбирать один и ют же центр приведения для всех гел системы, то для каждою из тел получим следующие условия равновесия
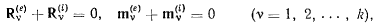
где 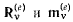 соответственно результирующая сила и момент результирующей пары всех сил, действующих на данное тело, кроме сил взаимодействия между отдельными телами (внутренних реакций).
соответственно результирующая сила и момент результирующей пары всех сил, действующих на данное тело, кроме сил взаимодействия между отдельными телами (внутренних реакций). 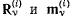 — соответственно результирующая сила и момент результирующей пары сил внутренних реакций, действующих на данное тело. Производя теперь формальное суммирование и принимая во внимание, что для внутренних сил взаимодействия выполняются условия
— соответственно результирующая сила и момент результирующей пары сил внутренних реакций, действующих на данное тело. Производя теперь формальное суммирование и принимая во внимание, что для внутренних сил взаимодействия выполняются условия
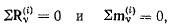
получим следующие необходимые условия равновесия системы твердых тел:
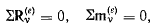
где суммирование уже распространяется на все точки взаимодействующих тел.
Пример:
Система состоит из двух однородных стержней CD длиной 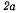 и OA длиной
и OA длиной 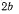 и весом Р. Оба стержня могут вращаться в одной вертикальной плоскости: стержень CD вокруг своей середины
и весом Р. Оба стержня могут вращаться в одной вертикальной плоскости: стержень CD вокруг своей середины 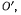 а стержень OA вокруг шарнира О, расположенною на одной вертикали с
а стержень OA вокруг шарнира О, расположенною на одной вертикали с 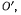 на расстояния
на расстояния 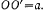 К концу D стержня CD подвешен груз весом Q. Груз Q посредством стержня CD отклоняет стержень OA от вертикального положения. Определить угол
К концу D стержня CD подвешен груз весом Q. Груз Q посредством стержня CD отклоняет стержень OA от вертикального положения. Определить угол 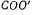 в положении равновесия системы, а также реакцию в точке О (рис. 99).
в положении равновесия системы, а также реакцию в точке О (рис. 99).
Решение:
Рассматриваемая система состоит из двух твердых стержней, находящихся под действием плоской системы сил. Условия равновесия первого стержня
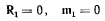
можно переписать в виде
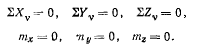
Последнее уравнение первой группы свидетельствует о том, что единственная сила реакции 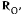 расположена в плоскости чертежа. Следовательно, момент результирующей пары направлен вдоль оси z, перпендикулярной к плоскости
расположена в плоскости чертежа. Следовательно, момент результирующей пары направлен вдоль оси z, перпендикулярной к плоскости 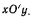 Рассматривая условия равновесия стержня OA, заметим, что и реакция в точке О расположена в плоскости чертежа, а условия равновесия каждого из стержней состоят из трех уравнений. В результате получим шесть уравнений равновесия системы для определения угла
Рассматривая условия равновесия стержня OA, заметим, что и реакция в точке О расположена в плоскости чертежа, а условия равновесия каждого из стержней состоят из трех уравнений. В результате получим шесть уравнений равновесия системы для определения угла 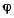 реакции в точках
реакции в точках 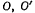 Для определения положения равновесия системы необходимо найти только одну величину — угол
Для определения положения равновесия системы необходимо найти только одну величину — угол 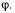
При составлении уравнений равновесия можно заметить, что они содержат но нескольку неизвестных величин (параметр 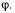 и неизвестные реакции).
и неизвестные реакции).
В зависимости от выбора центра приведения эти уравнения будут иметь более или менее сложный вид.
Рассмотрим сначала равновесие стержня 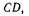 выбирая за центр приведения точку
выбирая за центр приведения точку 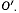 Условием равновесия является равенство нулю суммы моментов пар от приведения сил
Условием равновесия является равенство нулю суммы моментов пар от приведения сил 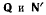 к точке
к точке 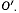 (здесь
(здесь 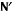 сила реакции, действующая со стороны стержня OA на стержень CD)
сила реакции, действующая со стороны стержня OA на стержень CD)
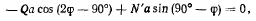
или
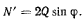
Перейдем теперь к исследованию равновесия стержня OA. За центр приведения выберем точку О, так что условие равновесия (равенство нулю суммы моментов пар при приведении к точке О) получит вид
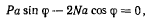
или
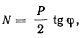
где .V—сила реакции, действующая со стороны стержня CD на OA. По третьему закону Ньютона  откуда
откуда
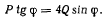
Полученное уравнение имеет два решения:
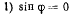
соответствует вертикальному положению стержней OA и CD; 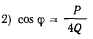
возможно лишь при условии
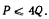
Тогда реакцию N в точке С получим в виде
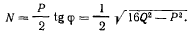
Для определения реакции в точке О рассмотрим сумму проекций сил. действующих на стержень OA, на горизонтальную и вертикальную оси
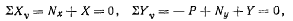
где X и У — проекции сил реакции в точке О. Отсюда получим
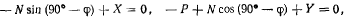
или
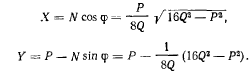
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:

