Условия равновесия системы сходящихся сил
Всякая система сходящихся сил может быть заменена равнодействующей, равной ее главному вектору. Если система сходящихся сил находится в равновесии, то ее равнодействующая, а следовательно, и ее главный вектор должны равняться нулю.
Соответственно двум способам определения главного вектора условие равновесия системы сходящихся сил может быть выражено в двух формах.
- Условие равновесия в геометрической форме. Геометрически главный вектор системы сил определяется как замыкающая сторона силового многоугольника. Для того чтобы он равнялся нулю, нужно, чтобы равнялась пулю замыкающая сторона силового многоугольника, т. е. конец последней силы в этом многоугольнике должен совпадать с началом первой силы. Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный для этой системы, был замкнутым.
- Условия равновесия в аналитической форме. Модуль главного вектора пространственой системы сил определяется формулой (8):
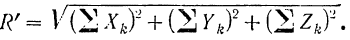
Но если 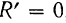 , то равно нулю и подкоренное выражение. Так как стоящие под корнем слагаемые как квадраты некоторых чисел всегда неотрицательны, то
, то равно нулю и подкоренное выражение. Так как стоящие под корнем слагаемые как квадраты некоторых чисел всегда неотрицательны, то 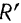 может равняться нулю только в том случае, если каждое из этих слагаемых равно нулю в отдельности:
может равняться нулю только в том случае, если каждое из этих слагаемых равно нулю в отдельности:
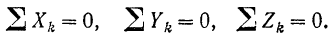
Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы порознь равнялись нулю суммы проекций всех сил на каждую из любых трех взаимно перпендикулярных осей.
В случае плоской системы сил, если координатные оси 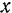 и
и 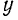 расположить в плоскости действия данных сил, третье уравнение равновесия обращается в тождество 0 = 0 при любых значениях сил, и потому для равновесия плоской системы сил достаточно выполнения лишь двух уравнений:
расположить в плоскости действия данных сил, третье уравнение равновесия обращается в тождество 0 = 0 при любых значениях сил, и потому для равновесия плоской системы сил достаточно выполнения лишь двух уравнений:
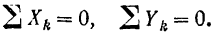
Для равновесия плоской системы сходящихся сил не-обходимо и достаточно, чтобы порознь равнялись нулю суммы проекций всех сил на каждую из любых двух взаимно перпендикулярных осей, лежащих в плоскости действия данных сил.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

