Оглавление:



Условия равновесия произвольной пространственной системы сил. Система параллельных сил. Система сходящихся сил
- Условие равновесия любой пространственной системы сил. Система параллельного питания. Система сходящихся сил теорема. Для равновесия свободного твердого тела под действием пространственной системы любой силы необходимо знать, что главный вектор и главный момент этой системы для любой точки равны нулю.: = = L4S=2m s(7, () = O. (6.8) К=Л к=\ Доказательство необходимости. В предыдущем параграфе, LGL^O или L4c # == # 0,
было доказано, что сила любой пространственной системы равна либо равнодействующей силе, либо паре сил, либо динамо-машине. Очевидно, что во всех этих случаях твердое тело не приходит в равновесное состояние. Поэтому для равновесия любой пространственной динамической системы необходимо выполнить условия (6.8). Доказательство адекватности.
Этих предпосылок, по-видимому, недостаточно, потому что при их выполнении все Людмила Фирмаль
заданные силы переносятся в точку С, и все объединенные пары уравновешиваются. Условие равновесия (6.8) также может быть записано проекцией на координатные оси: п п п п п / * ГЛ. x=2= — 2FkV=g = 2=O’/?=1/?=1k = l (6.9) M S x=S L1X=0. M S I (Fk)=o, — L=1=1 / g=1 Поэтому под действием сил любой пространственной системы, обусловленных равновесием свободных твердых тел Необходимо, чтобы алгебраическая сумма проекций всех сил для каждой из трех
осей и сумма моментов всех сил для каждой из трех осей равнялась нулю, следовательно, число независимых уравнений равновесия сил любой пространственной системы не превышает шести. Другими словами, для одного свободного твердого тела, в котором рассматривается равновесие, невозможно построить более шести независимых уравнений равновесия. Физическая сущность полученного
- уравнения равновесия (6.9) становится более ясной, когда мы вводим новое понятие-степени свободы. Степень свободы тела или системы тела-это число независимых геометрических параметров, которые идеально определяют положение тела. Свободное твердое тело Вселенной имеет шесть степеней свободы. Таким образом, число уравнений равновесия данной силы равно числу степеней свободы данного тела или системы тел, так как оно может перемещаться и вращаться относительно трех взаимно перпендикулярных
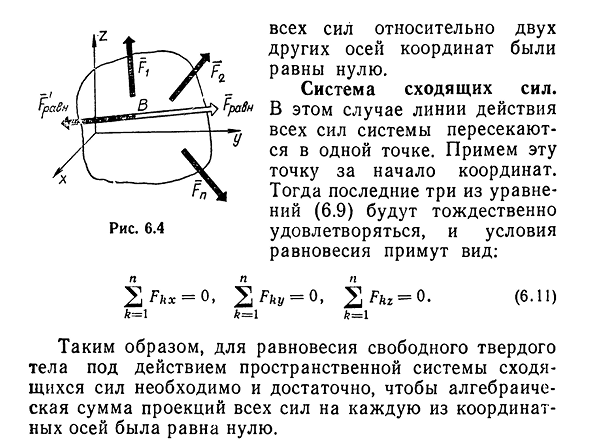
координатных осей. Рассмотрим специальный пример.^Система параллельных сил. Пусть{F \ t F2i…f FN} — система параллельных сил в пространстве. Пользуясь тем, что координатные оси могут быть произвольно размещены в пространстве, ось z направлена параллельно линии действия системы параллельных сил. Тогда проекция всех сил системы на оси x и y и их моментов на оси z будет равна нулю, а условие (6.9) будет иметь вид: 2 / ^=0,2}L1x(RL)=0,S^(f)=0. (6.10)A-1L=1fe=l Таким образом, для равновесия свободных твердых тел под действием пространственной системы параллельных сил алгебраическая сумма проекций всех сил на ось,
параллельную их линии действия, и сумма сил, параллельных друг другу. Харрис 6.4 Людмила Фирмаль
Все силы для двух других осей были равны нулю. Система нисходящей силы. В этом случае линии действия всех сил системы пересекаются в одной точке. Пожалуйста, используйте этот пункт в качестве источника. Тогда последние три уравнения (6.9) удовлетворяются таким же образом, и условие равновесия принимает вид: n2Fftx=0, k=\ %F k y=0, k = l Ffcz2=0. fc = l (6.11) Таким образом, для равновесия свободного твердого тела под действием пространственной системы сходящихся сил необходимо, чтобы алгебраическая сумма проекций всех сил на каждую координатную ось была равна нулю.
Смотрите также:

