Оглавление:
Условия независимости криволинейного интеграла II рода от пути интегрирования
Пусть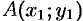 
и 
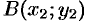— две произвольные точки односвязной области 
плоскости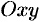 
(область называется односвязной, если для любого замкнутого контура, лежащего в этой области, ограниченная им часть плоскости целиком принадлежит (области без «дыр»)). Точки 
и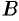 
можно соединить различными линиями (на рис. 242 это 
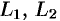и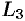 
). По каждой из этих кривых интеграл
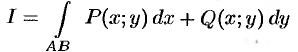
имеет, вообще говоря, свое значение.
Если же его значения по всевозможным кривым 
одинаковы, то говорят, что интеграл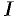 
не зависит от вида пути интегрирования. В этом случае для интеграла 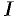достаточно отметить лишь его начальную точку 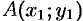и его конечную точку 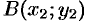пути. Записывают:
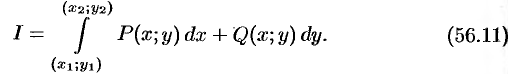
Каковы же условия, при которых криволинейный интеграл II рода не зависел от вида пути интегрирования?
Теорема 56.3. Для того чтобы криволинейный интеграл
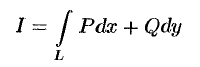
не зависел от пути интегрирования в односвязной области , в которой функции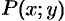 
, 
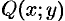, непрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие
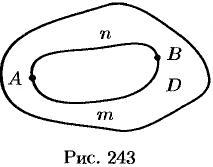
Докажем достаточность условия (56.12). Рассмотрим произвольный замкнутый контур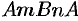 
(или 
) в области (см. рис. 243). Для него имеет место формула Остроградского-Грина (56.8). В силу условия (56.12) имеем:
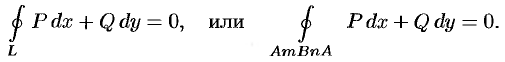
Учитывая свойства криволинейного интеграла, имеем:
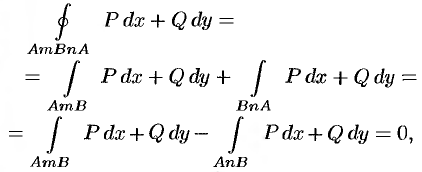
т.е.
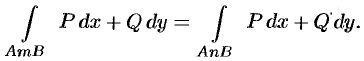
Полученное равенство означает, что криволинейный интеграл не зависит от нуги интегрирования.
В ходе доказательства теоремы получено, что если выполняется условие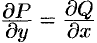 
, то интеграл по замкнутому контуру равен нулю:
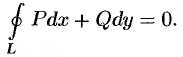
Верно и обратное утверждение.
Следствие 56.1. Если выполнено условие (56.12). то подынтегральное выражение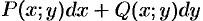 
является полным дифференциалом некоторой функции 
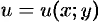(см. (44.5)), т. е.
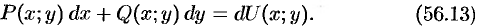
Тогда (см. (56.11)):
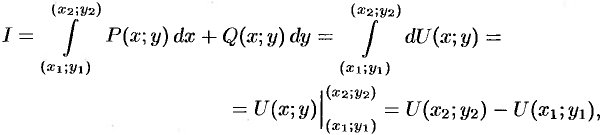
т.е.
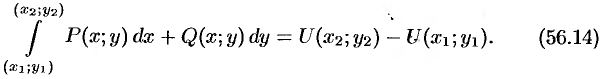
Формула (56.14) называется обобщенной формулой Ньютона Лейбница для криволинейного интеграла от полного дифференциала.
Следствие 56.2. Если подынтегральное выражение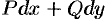 
есть полный дифференциал и путь интегрирования замкнутый, то
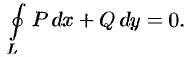
Замечания.
1. Чтобы не спутать переменную интегрирования 
с верхним пределом , переменную интегрирования обозначают другой буквой (например,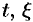 
и т.д.).
2. Функцию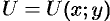 
, удовлетворяющую условию (56.12), можно найти, используя формулу
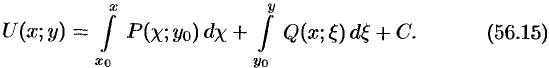
В качестве начальной точки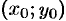 
обычно берут точку (0; 0) — начало координат (см. пример 56.5).
3. Аналогичные результаты справедливы для криволинейного интеграла
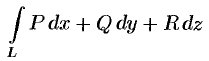
по пространственной кривой. Условие (56.12), равенство (56.13), формулы (56.14) и (56.15) имеют соответственно вид:
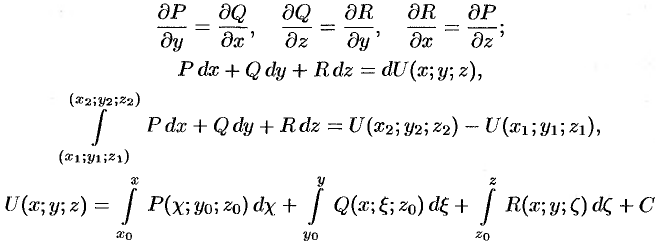
(см. пример 73.1).
Пример №56.4.
Найти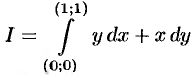 
.
Решение:
Здесь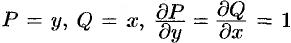 
. Согласно вышеприведенной теореме, интеграл не зависит от пути интегрирования. В качестве пути интегрирования можно взять отрезок прямой 
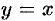, дугу параболы 
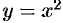и т. д. или воспользоваться формулой (56.14). Так как 
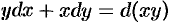, то
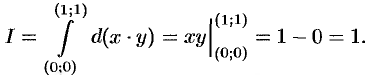
Пример №56.5.
Убедиться, что выражение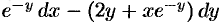 
представляет собой полный дифференциал некоторой функции 
и найти ее.
Решение:
Для того чтобы указанное выражение являлось полным дифференциалом, необходимо выполнение условий (56.12):
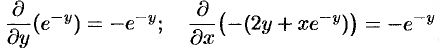
— условия выполнены, следовательно,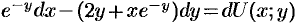 
. А так как полный дифференциал имеет вид
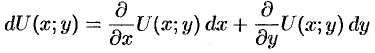
(см. п. 44.3), то верны соотношения
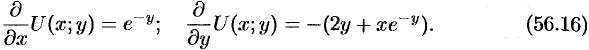
Интегрируем по первое из уравнений, считая 
постоянным, при этом вместо постоянной интегрирования следует поставить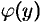 
— неизвестную функцию, зависящую только от :
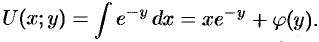
Подставляя полученное выражение во второе из уравнений (56.16), найдем :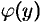
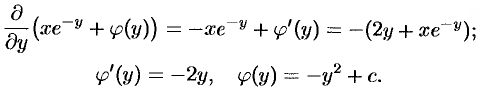
Таким образом,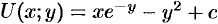 
.
Отметим, что функцию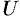 
проще найти, используя формулу (56.15):
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Вычисление криволинейного интеграла II рода |
| Формула Остроградского-Грина |
| Некоторые приложения криволинейного интеграла II рода |
| Вычисление поверхностного интеграла I рода |
