Оглавление:


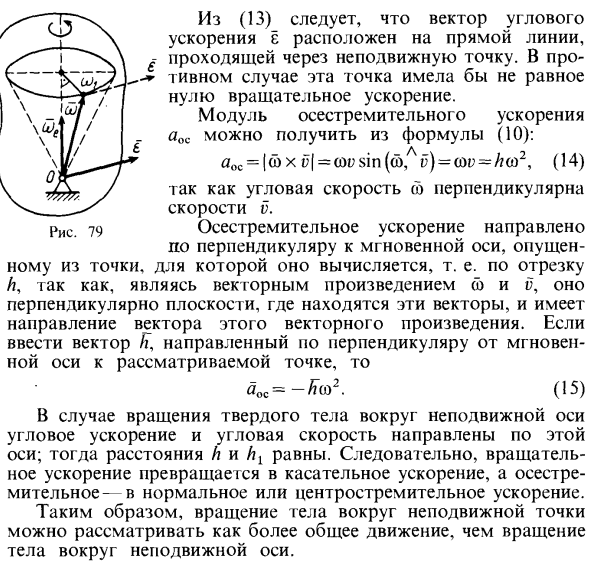

Ускорения точек тела при вращении вокруг неподвижной точки
- Уравнение ускорения точки M объекта, вращающегося вокруг неподвижной точки, не может быть получено непосредственно с использованием уравнения ускорения вращательного движения вокруг неподвижной оси. В рассматриваемом случае угловое ускорение е обычно не направлено вдоль оси вращения, и, как следствие, направлено вдоль оси. Во всех остальных отношениях уравнения ускорения в этих случаях полностью аналогичны.
Уравнение для ускорения точки на теле M может быть получено путем дифференцирования вектора скорости по времени, принимая во внимание, что скорость вычисляется по уравнению (2). Когда эта дифференциация выполняется, a = du / dz = dcb / dr x f + / dz = e; df / dt = v = (окс, тогда a = yohg + yhi. (8) Формула (8) называется формулой соперника. Часть общего ускорения D.► = Йог (9) Другая часть называется ускорением вращения ак = шхр (10) -Удержанное ускорение. Таким образом, уравнение (8) принимает вид: a = a.P + «a, (P) Другими словами, ускорение точки объекта, которая вращается вокруг фиксированной точки, равно векторной сумме ускорения вращения и непрерывного ускорения.
Но в какой-то данный момент движущая сила или полезное сопротивление, например, стремится установить другой режим или другую среднюю скорость. Людмила Фирмаль
В общем, ускорение вращения и устойчивое ускорение не являются вертикальными. Поэтому коэффициент ускорения а рассчитывается как диагональ параллелограмма по формуле a = + a «+ 2a» p «os cos (Avr Ha») • (12) Рассмотрим ускорение вращения и устойчивое ускорение отдельно. Вращательное ускорение рассчитывается по уравнению (9), аналогично точечному уравнению скорости (2). Только здесь вводится угловое ускорение e вместо угловой скорости ω. Таким образом, если тело вращается мгновенно с угловой скоростью, равной угловому ускорению e, вращательное ускорение dvr направлено так же, как скорость v.
- Модуль ATS ускорения вращения определяется так же, как и модуль v скорости [справочная формула (3)]: D «p = A1E, (13). Где d — кратчайшее расстояние от точки тела до линии, на которую направлено угловое ускорение e (рис. 79). Выражение avr (13) получается из (9). dvr = I e x f | = er sin (e, r) = d, e, где rsinfo r) = d1. Из (13) видно, что вектор углового ускорения ξ находится на прямой, проходящей через неподвижную точку. В противном случае ускорение вращения в этой точке не равно нулю. Модуль осторожен. г ………….. АОС можно получить из уравнения (10). aos = | yx v [= ) = = A <o2, (14).
Поскольку угловая скорость перпендикулярна скорости V Сильное ускорение направлено перпендикулярно мгновенной оси и опущено. Поэтому он рассчитывается по сегменту ускорение С точки зрения „……. r …… _ …….. h, поскольку эти векторы являются векторными произведениями, перпендикулярными плоскости, в которой они расположены, они имеют векторное направление этого векторного произведения Если ввести вектор и навести его перпендикулярно от мгновенной оси a <k = -u <n2. ( «5).
Учитывая движение Земли вокруг Солнца, ее можно считать абсолютно твердым телом, но на самом деле это не твердое тело, а морская, воздушная оболочка и т. Людмила Фирмаль
Для вращения твердого тела вокруг неподвижной оси угловое ускорение и угловая скорость направлены вдоль этой оси. Расстояния h и ht равны. В результате вращательное ускорение изменяется на тангенциальное ускорение, а одиночное ускорение изменяется на нормальное или центростремительное ускорение. Следовательно, вращение объекта вокруг фиксированной точки можно рассматривать как более общее движение, чем вращение объекта вокруг фиксированной оси.
Смотрите также:
Задачи по теоретической механике
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

