Ускорение точки
Ускорение точки — это характеристика движения точки, которая определяет изменение вектора скорости по величине и по направлению.
Если точка движется равнопеременно и по прямой линии, то величина ускорения определяется делением изменения скорости на время,
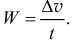
В общем же случае определение ускорения зависит от способа задания движения точки.
Ускорение точки при векторном способе задании движении. Пусть за время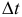 
точка перешла из положения 
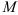в 
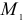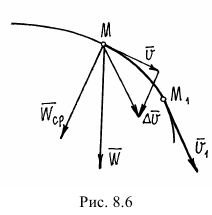
, и за это время вектор скорости изменился на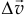 
(рис. 8.6).
Полагая из-за малости времени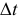 
дугу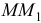 
почти прямой, а движение близким к равнопеременному, найдём приближенное среднее ускорение 
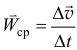(так как 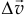— вектор, то и 
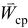— вектор, направленный параллельно 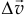). Конечно, чем меньше 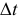, тем точнее будет определено ускорение. Поэтому точное ускорение
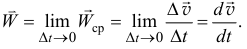
Следовательно, ускорение точки есть производная от вектора скорости или вторая производная от радиуса-вектора точки по времени
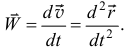
Направление вектора ускорения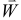 
можно определить как предельное положение вектора 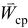при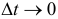 
. Нетрудно обнаружить, что ускорение не направлено по касательной, а направлено, вероятно, в сторону вогнутости траектории (см. рис. 8.6).
Ускорение точки при координатном способе задания движения.
Подставив в (8.5) выражение радиуса-вектора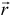 
через координаты (8.1), получим:
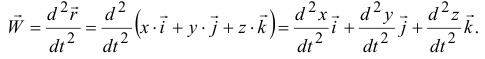
Отсюда следует, что проекции вектора ускорения на оси равны вторым производным по времени от соответствующих координат точки
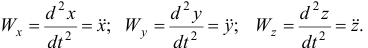
Поэтому модуль вектора ускорения
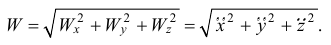
Направление вектора можно найти или графическим способом, откладывая в масштабе составляющие параллельно осям с учётом знака, или с помощью направляющих косинусов:
(
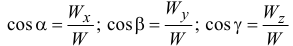
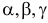— углы между вектором 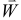и направлениями осей 
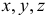соответственно).
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Способы задания движения точки |
| Скорость точки |
| Поступательное движение тела |
| Вращение тела вокруг неподвижной оси |
