Оглавление:



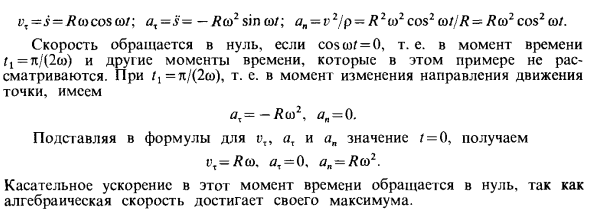

Ускорение точки при естественном способе задания движения
- Для точечной скорости, Согласно определению ускорения. Мы получаем Это связано с тем, что y2 = n2 и dx / dz ориентированы на вогнутой поверхности траектории параллельно главному нормальному единичному вектору. Разлагает точечные ускорения вдоль оси естественного трехгранника. Блок ускорения at = ST = (dut / dz) T. Это называется тангенциальной составляющей ускорения. Другие части ускорения a „= (c2 / p) n = (s2 / p>. Это называется нормальной составляющей ускорения.
Он ориентирован внутри вогнутой поверхности траектории, то есть в положительном направлении единичного вектора основной нормали l. Это потому, что полное ускорение направлено внутрь вогнутой поверхности орбиты. Следовательно, ускорение очков Из (17) получим формулу для проекции ускорения на естественную ось. У нас есть: a, = s = dvt / dT, a = tr / p, ab = 0. (19) Проекция ускорения в направлении касательной, которая совпадает с направлением единичного вектора m, называется тангенциальным ускорением и является нормальным ускорением ускорения на главной нормали, направленной вдоль единичного вектора. Проекция ускорения на бинормальную линию вдоль единичного вектора B равна нулю. Таким образом, точечное ускорение находится на контактной поверхности дорожки.
Реальная природа принципа виртуальной скорости заключается в том, что этот принцип является, так сказать, общей формулой, решающей задачу статики, и поэтому он становится альтернативой другим принципам. Людмила Фирмаль
Эта плоскость имеет касательные и главные нормальные единичные векторы. Учитывая ортогональность а и а (рис. 17), согласно уравнению (18) lg «. | a, | / a, (20) Нормальная составляющая ускорения а всегда направлена внутрь вогнутой поверхности орбиты. Касательная составляющая a с 5> 0 направлена в положительную сторону касательной, то есть в направлении единичного вектора m, а когда s <0, она направлена в отрицательном направлении, противоположном t. При 5> 0 и j ‘> 0 вектор скорости и тангенциальная составляющая ускорения направлены в одну сторону вдоль точки. Движение точки ускоряется в положительном направлении касательной к траектории.
Если s <0 и s <0, направление вектора скорости и тангенциальная составляющая ускорения совпадают, поэтому движение точки ускоряется, но в отрицательном направлении касательной к траектории. Если i> 0 и 5 <0, вектор скорости ориентирован вдоль m, а вектор касательных к ускорению противоположен направлению. Движение точки замедляется в положительном направлении, касательном к траектории. s Если <0 и $> 0, происходит медленное движение точки в отрицательном направлении, касательном к траектории точки. Если тангенциальное ускорение исчезнет, оно будет взято из условия AT-DV, / DT = 0.
- Это условие всегда выполняется, но = | и | = const, т. Е. Когда точка движется равномерно по траектории любой формы. Касательное ускорение также исчезает, когда алгебраическая скорость v достигает предельного значения, например максимального или минимального значения. Изменение в алгебраической скорости как функция 18 часов для того, что показано на рисунке, тангенциальное ускорение равно Ноль в моменты времени r и t2. Во время вибрации маятника (рис. 19) эти моменты соответствуют прохождению через точку А. Когда маятник движется в одном направлении, алгебраическая скорость в точке A максимизируется, а когда он движется в противоположном направлении, она минимизируется. Для нормализации до нуля Ускорение продолжается от условий 4 = 2 / P = 0- Это условие выполняется при p = oo.
Другими словами, это линейное движение точек. Когда точка движется по кривой траектории, p = oo в точке перегиба, где выпуклая поверхность траектории меняется на вогнутую поверхность, и наоборот (рисунок 20). Нормальное ускорение исчезает, когда u = 0, то есть когда направление точки движется вдоль траектории. В случае маятника такой момент является моментом вылета Маятник под максимальным углом как в одном направлении, так и в другом. Эти моменты соответствуют моментам Новое в маятнике.
Любая геодезическая линия, проведенная на вытянутом эллипсоиде вращения, представляет собой helpoloform, который может быть образован эллипсом с центральным качением, закрепленным вдоль этой плоскости. Людмила Фирмаль
Случай обработки т * 0 Рис. 21 Тангенциальное ускорение и нормальное ускорение ноль и их общая формула указывают, что тангенциальное ускорение характеризует изменение величины вектора скорости и изменение направления нормали. Пример. Точка движется по дуге окружности радиуса R по закону s = R-sinωr (где ω = const). Начните считать расстояние и время. Направление положительного расстояния также показано на рисунке. 21. Определите скорость Ускорение в момент времени I и значения в точке О и точке орбиты М скорость исчезает.
Решения. Проекция скорости и ускорения на естественную ось определяется уравнениями (16) и (19). У нас есть: i /, = i = R t; a, = s = -Яш2sinш /; a „-vi / p-R2 l / R = Ra> cosa> f = 0, то есть t1 = π Мы смотрим на этот пример, где скорость исчезает при / (2a>): /, = i / (2y), то есть в момент изменения направления точки, , = -H2, a, = 0. «Получить выражения a и a, r = 0, 1>, = Jash. A, = 0. a„ = R <o2. Поскольку алгебраическая скорость достигает максимума, тангенциальное ускорение в этой точке исчезает.
Смотрите также:
Задачи по теоретической механике
| Естественный трехгранник | Частные случаи движения точки |
| Дифференцирование единичного вектора | Скорость и ускорение точки в полярных координатах |
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

