Ускорение точки

Ускорение точки. Проекции ускорения на прямоугольные оси координат.

Рассматривая движение материальной точки, мы определили вектор v скорости этой точки. Перенесем вектор v в начало неподвижной системы осей 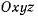(рис. 28).

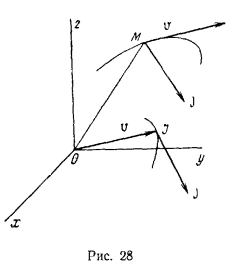
Конец 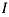этого нового вектора назовем индексом скорости точки. При движении точки по траектории вектор v скорости будет изменять свои величину и направление, при этом индекс 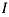скорости точки будет описывать некоторую кривую относительно системы отсчета 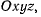которую будем называть годографом скорости точки. Обозначив через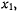 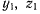координаты индекса скорости, приходим к очевидным соотношениям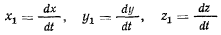

Вектор скорости движения индекса 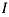по годографу обозначим через 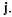Тогда проекции вектора 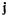определяется из равенств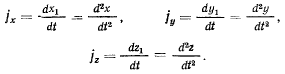

Вектор 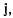приложенный к точке М, называется ускорением точки М. Скорость точки М определяется через производную от ее радиус-вектора

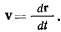
Вектор ускорения точки определяется как скорость движения индекса по годографу скорости и в соответствии с определением производной от вектора, получим

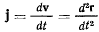
(в самом определении производной от вектора по скалярному аргументу содержится условие переноса вектора в начало координат). Величина вектора ускорения точки может быть выражена через проекции на ортогональные оси координат следующим образом:

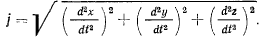
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Принцип Даламбера

Кинематика точки

Скорость и ускорение точки в полярных координатах

Движение точки по окружности