Оглавление:
Ускорение точки. Его определение при задании движения точки векторным способом
Движение точки с неизменной по модулю и направлению скоростью (равномерное прямолинейное движение) встречается на практике сравнительно редко. В подавляющем большинстве случаев скорость точки при движении изменяется. Для того чтобы установить в динамике зависимость между изменением движения тела и силами, действующими на тело, нужно как-то охарактеризовать изменение движения и установить меру этого изменения.
Величина, характеризующая быстроту изменения скорости точки (как по модулю, так и по направлению), называется ускорением точки.
Пусть точка, движущаяся по некоторой криволинейной траектории (рис. 106), занимает на ней в момент времени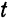 
положение 
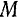и в момент 
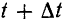— положение 
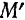. Скорости 
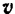и 
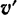точки в ее положениях 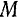и 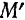будут направлены по соответствующим касательным.
Определим изменение скорости точки за промежуток времени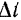 
, т. е. при переходе точки из положения 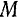в положение 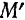. Перенесем для этого начало вектора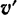
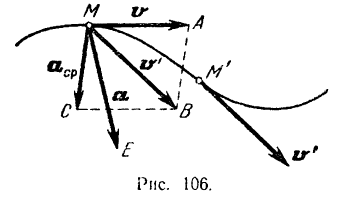
в точку 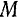, соединим концы 
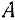и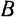 
векторов 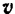и 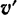и дополним полученный треугольник 
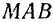до параллелограмма 
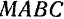. Вектор 
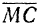является геометрической разностью векторов 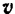и .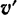
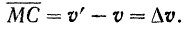
Вектор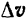 
, представляющий собой геометрическую разность векторов скорости точки в конце и начале данного промежутка времени, называется приращением скорости точки за соответствующий промежуток времени.
Вектор 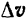вполне определяет и по модулю, и по направлению происшедшее за время 
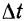изменение скорости движущейся точки, поэтому отношение этого вектора к данному промежутку времени принимается за среднее ускорение точки за соответствующий промежуток времени.
Обозначив среднее ускорение точки символом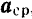 
, будем иметь:
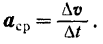
Среднее ускорение точки позволяет судить только о конечном изменении скорости точки за рассматриваемый промежуток времени и не дает представления о действительном изменении величины и направления скорости точки в каждый момент. Каждому новому промежутку времени 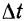будет соответствовать свое положение точки 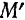на траектории и, вообще говоря, свое направление и своя величина скорости 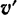точки. Изменению вектора 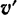будет соответствовать изменение и вектора 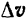приращения скорости за рассматриваемый промежуток времени.
Очевидно, что вектор а ускорения точки в данный момент времени равен пределу среднего ускорения точки за промежуток времени, начинающийся в этот момент, когда величина промежутка времени стремится к нулю:
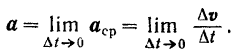
Так как скорость 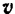точки есть векторная функция времени, то
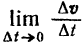
есть векторная производная этой функции.
Следовательно:
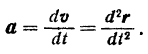
Ускорение точки равно первой производной от скорости или второй производной от радиуса-вектора точки по времени.
Важно заметить, что во всех случаях (за исключением прямолинейного движения) модуль ускорения точки, равный модулю производной от скорости 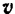по времени, не равен производной от модуля v скорости по времени.
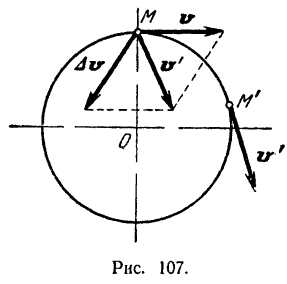
Так, например, при равномерном движении тачки по окружности модуль ее скорости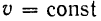 
и потому 
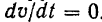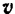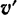. Векторы же и скорости точки (рис. 107) различны по направлению и потому 
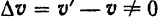. Следовательно, модуль ускорения точки
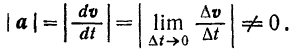
Размерность ускорения
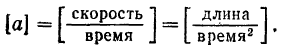
Каждому выбору единицы длины и единицы времени соответствует своя единица ускорения.
Ускорение может выражаться в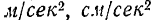 
и т. д.
Пример задачи:
Задано векторное уравнение движения точки
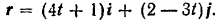
Определить траекторию, скорость и ускорение данной точки.
Решение:
Траектория точки есть линия, определяемая параметрическими уравнениями
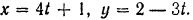
Исключая из них параметр (время)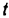 
, получим:
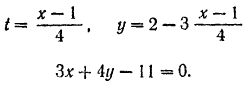
В начальный момент, при
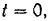
координаты точки
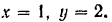
Следовательно, траектория точки есть полупрямая, определяемая уравнением
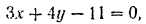
с началом в точке
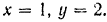
Скорость и ускорение точки находим по формулам (57) и (59). как первую и вторую производную от вектора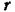 
по :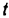
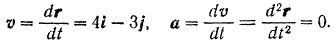
Следовательно. точка движется по прямой с постоянной скоростью, модуль которой
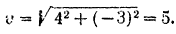
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
