Ускорение точки — Физическая величина

Ускорение точки

• Равномерное линейное движение характеризуется величиной только одной точки-скоростью, которая в течение всего движения точки остается постоянной. В криволинейном движении скорость точек различна в разное время. Даже если значение скорости не изменяется, все равно происходит изменение направления скорости. В общем случае скорость изменяется как по величине, так и по

направлению. Для характеристики неравномерного движения необходимо значение, указывающее численное значение скорости точки и скорости изменения направления. Это значение называется ускорением точки. Рассмотрим естественный способ установки движения. Пусть, например, точка перемещается в криволинейной форме(рис. 9.13), находился в какой-то момент времени t в положении M и имел скорость, а через короткий промежуток

времени&t=ti-t-изменение положения Mi и скорости CR для построения вектора V и Людмила Фирмаль

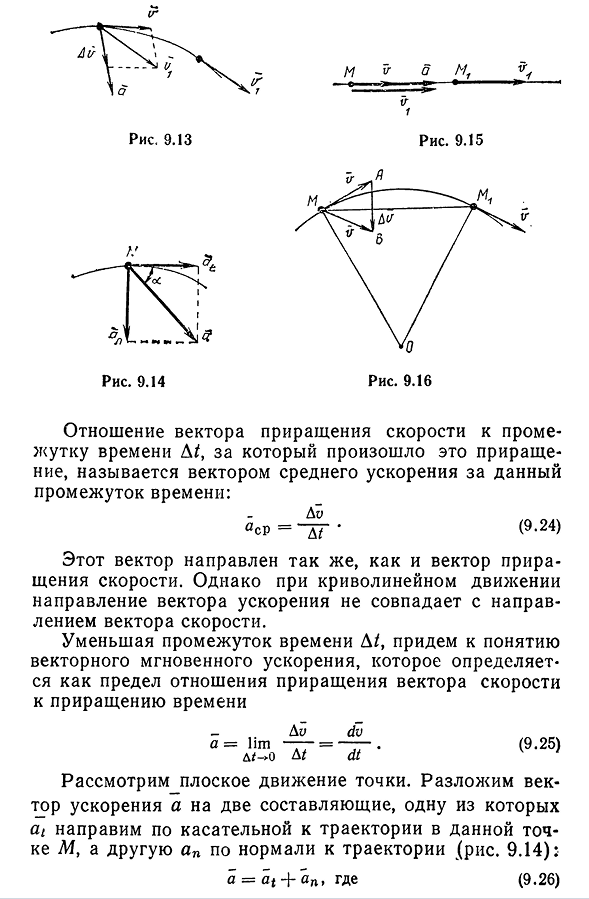
точки M параллелограмма диагональю является вектор, а одной стороной-вектор V.: D u^s^ — u. (9.23) 87.3. 9.14 тн1 И в М1 Отношение вектора приращения скорости к временному интервалу, в котором произошло это приращение, называется средним вектором ускорения для указанного временного интервала: Дистанционное управление И CP=D/*(9.24) этот вектор обозначается так же, как вектор приращения

скорости. Однако в криволинейном движении направление вектора ускорения не совпадает с направлением вектора скорости. Уменьшение временного интервала D / делает вектор мгновенного ускорения понятием, определяемым как предел отношения приращения к приращению вектора скорости Du dv a = lim» — = ———. о компании d/ — >D / dt (9.25 )) Рассмотрим плоское движение точек. Разложим вектор ускорения а на две составляющие, одна из которых тангенциально ориентирована к орбите этой точки М, а другая АП перпендикулярна орбите(рис. 9.14): a=at+ant, где(9.26) 88at называетс

• я тангенциальным или касательным ускорением, а АП^нормальное или центростремительное ускорение. В линейном движении вектор скорости всегда направлен вдоль линии, по которой движется точка. Ясно, что направление ускорения совпадает с направлением вектора Di на фиг. 9.15). В этом случае проекция ускорения точки на Нормаль на траектории равна нулю(AP=0 ): а=в+в=в. (9.27 Модуль тангенциального вектора ускорения равен модулю временной производной скорости: Я Д2 я Я dt2g(9.28)) Тангенциальное ускорение характеризует изменение коэффициента скорости. Теперь рассмотрим равномерное движение точек по траектории кривой.

Предположим, что траектория движения представляет собой круг. Возьмите два более близких положения M и Mi движущейся точки. Скорость точки постоянна, но ее направление меняется. Найдите различия в этих скоростях, используя правила треугольника(рис. 9.16). Полученные равнобедренные треугольники OM M i и M A B похожи, потому что они имеют одинаковый угол в вершине. Из подобия треугольников, подобные стороны будут пропорциональны: Du / L4L41= = v/R t(9.29), где R-радиус окружности. В этом случае длина кода M M X стремится к длине дуги: MM1=IDL на пределе получаем Дю-дю-a1ip л л л/’=1Т~73 — = — * д / — >О, мм^Г/>О, Д/у ц

Ограничение (9.29) в правой части соотношения равно: Вот так оно и есть. о d/ — >R R Людмила Фирмаль

Затем alv=v / R t 89. a=v2 / R.(9.30) Направление вектора ускорения перпендикулярно хорде мм [t]предела (D/->0), а вектор ускорения направлен к центру окружности вдоль нормали траектории. Итак, в этом случае тангенциальное ускорение равно нулю, поэтому коэффициент нормального ускорения равен: = = = V2 / R.(9.31) В этом случае изменение скорости происходит только в направлении. Таким образом, обычное ускорение характеризует изменение только в направлении скорости точки. Если траектория точки — не окружность, а произвольная кривая, то в Формуле (9.31) вместо радиуса окружности пусть радиус кривизны кривой в этой точке равен p. эго возможно, так как можно заменить бесконечно малу

ю дугу кривой вблизи данной точки соответствующей дугой окружности. Из рисунка. 9.14 касательное, нормальное и полное ускорение не трудно найти связь между модулями: at1=Kos a;1U (9.32)AP=sin A. ) В свою очередь, полный модуль ускорения является геометрической суммой тангенциального и нормального ускорения: A2A2=a2cos2a -| — a2sin2a=A2 , Или a=Y a]+A2=V (dv/dt) 2+v2 / p. (9.33) Если движение точек задано координатами, то проекция ускорения на координатные оси представляется как первый дифференциал проекции скорости точек на эти оси: d2x dt* d2y dt2′ ДВЗ___ _ d2z скрыл=ДТ=ДТ*’ (9.34)) 90-модульное ускорение в этом случае представляется в виде а а2х+А2А2. (9.35 утра )) Направление

ускорения определяется из соотношения ПОТОМУ ЧТО потому что Когда точка движется по прямой линии в плоскости или в уравнении (9.35), члены az или AZ и AU равны нулю соответственно. Согласно системе СИ, ускорение выражается в квадратных метрах в секунду (м/с2). Например. Определите модули скорости, касательности, нормального и полного ускорения точки АФ, расположенной на краю колеса, которое равномерно катится без скольжения по прямой (рис. 9.7). Решение. Закон движения точки M приведен в предыдущем примере: s=2D[1-cos (vQt/D)], где y0-скорость вращения оси колеса, А D-диаметр колеса. Коэффициент скорости точки М по формуле (9.16)) =2C, Найти модуль тангенциального ускорения. Согласно формуле (9.28), мы имеем I ДВ Для нормального модуля ускорения (9.30) получаем Д (9.33) 2 Vo t I » 5-cos“ 1/2 Модуль Полного Ускорения 1 / 2j2 а=V В+Н= * «2 Sin~ ~ d~’ №«

Смотрите также:

Решение задач по технической механике

Введение в кинематику. Способы задания движения точки	Формула Эйлера
Скорость точки	Равномерное движение

Если вам потребуется заказать решение по технической механике вы всегда можете написать мне в whatsapp.