Оглавление:


Ускорение точки
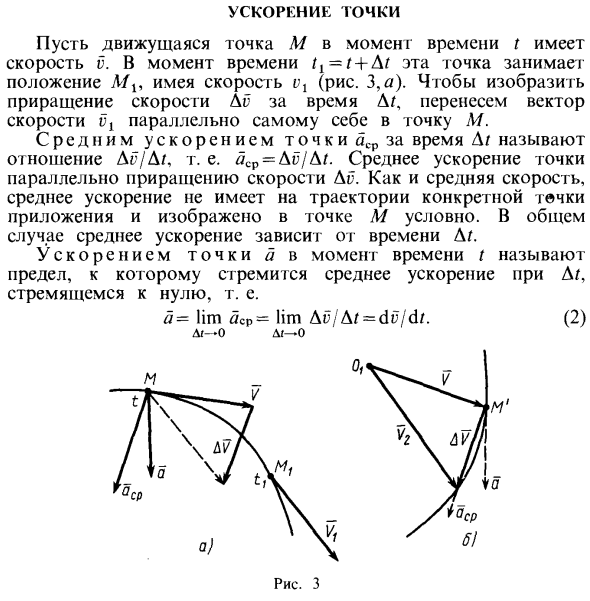
- Пусть V будет скоростью перемещения точки M в момент времени t. В момент времени tl = t + ^ t эта гонка занимает позицию скорости m (рисунок 3). Перенесите вектор скорости vl в точку M, параллельную себе, чтобы представить приращение скорости Дг за время Д /.
При применении теоремы об изменении момента движения для двух тел вращение объекта вокруг параллельной оси влечет за собой неизвестный импульсный момент в месте фиксации хотя бы одного из них на оси вращения. Людмила Фирмаль
Импульс за время Dm и среднее ускорение acr — это отношение Dg / Dm. То есть acv = \ vl \ t. Среднее ускорение точек параллельно скорости приращения Di. Как и средняя скорость, среднее ускорение не имеет определенной течки на траектории и обычно представлено точкой М. В общем случае среднее ускорение зависит от времени D /.
- Ускорение в точке а в момент времени t является пределом среднего ускорения, когда D / стремится к нулю. А-limСCp = Hm Dp / & t = dvjdt. (2) / И — о, о Рисунок 3 Следовательно, точечное ускорение равно первой производной точечной скорости. Увеличение скорости да, так что среднее ускорение направлено на вогнутую поверхность траектории. Предельное значение в L / также указано. Есть тенденция стать нулем.
Обычно мгновенный центр ускорения располагается в плоской фигуре, за исключением особых случаев, когда угловая скорость или угловое ускорение равны нулю, поэтому необходимо определить расстояние до рассматриваемой точки фигуры. Людмила Фирмаль
Таким образом, точка ускорения также направлена внутрь вогнутой поверхности траектории. Кроме того, ускорение как первая производная скорости, обусловленное характеристиками векторного годографа, параллельно тангенсу вектора скорости годографа (рис. 3.6). Измерение ускорения СИ можно получить из (2): [a] = [u] / [z] = скорость / время i = m / s2 = m • s ‘2.
Смотрите также:
Задачи по теоретической механике
| Объем полушара | Векторный способ изучения движения |
| Скорость точки | Координатный способ изучения движения |
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

