Оглавление:

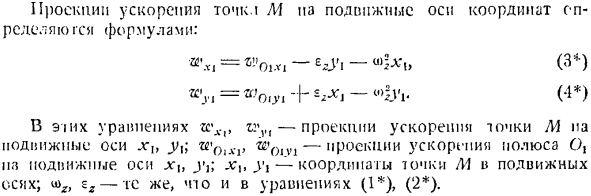













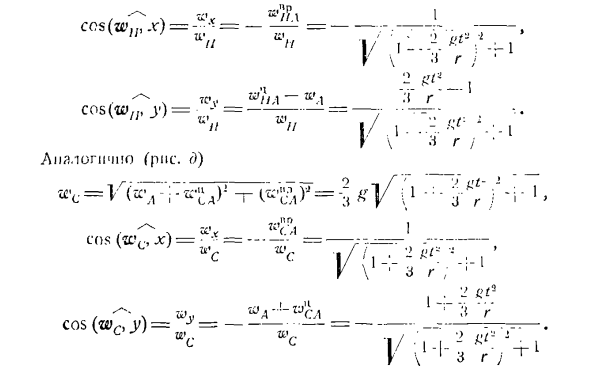






















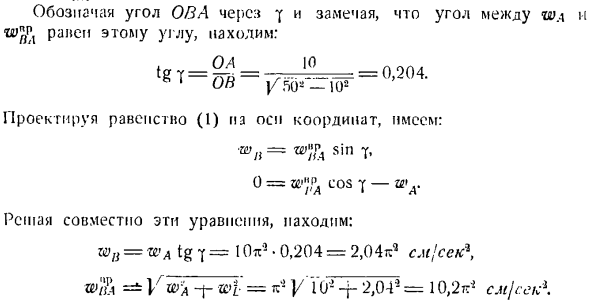













Ускорение точек плоской фигуры
- Ускорение точки плоской фигуры Ускорение точек на виде в плане можно определить с помощью анализа, анализа графиков и графических методов. В данном разделе описываются аналитические и графоаналитические методы определения точек ускорения на видах в плане.
L и метод Риги-Чески: проекция ускорения любой точки На плане этажа в фиксированную декартову координатную ось! Это уравнение.: (]*) (2 *) Я.* = Ъ > ГХ-е,0> — з вставить.(х-х(з)> в = «О * Г Е» *(Х-x0r) — ж *(г-y01). Проекция точки ускорения Эти выражения ПМР — Требовать cooelinate X, Y фиксированная ось. ©V)i * = = = a’Oi> woiy = yOi- Проекция ускорения полюсов на координатные оси не осуществляется(начало движения системы!! Координирует.) «> * = ) и (2) r легко найти. М. Так… па Рисунок 6.12.
Графический способ нахождения ускорения точки в плане заключается в построении плана ускорения и будет рассмотрен отдельно. Людмила Фирмаль
Если взять мгновенный центр ускорения относительно полюса, то ускорение любой точки На плане определяется по формуле: \ \ / =- ‘»Вчз» ХС,.(И) \ Х / ^^ ‘/ Ускорение любой точки (J — — — является радиус-вектором、 。От мгновенного центра ускорителя Тот же угол a(12). р»с<(jk; модуль ускорения плоского пятна Расстояние до мгновенного центра акселерометра ускорения (рисунок (>.!(;).Значение ускорения равно、 уа = р-р] (15 )
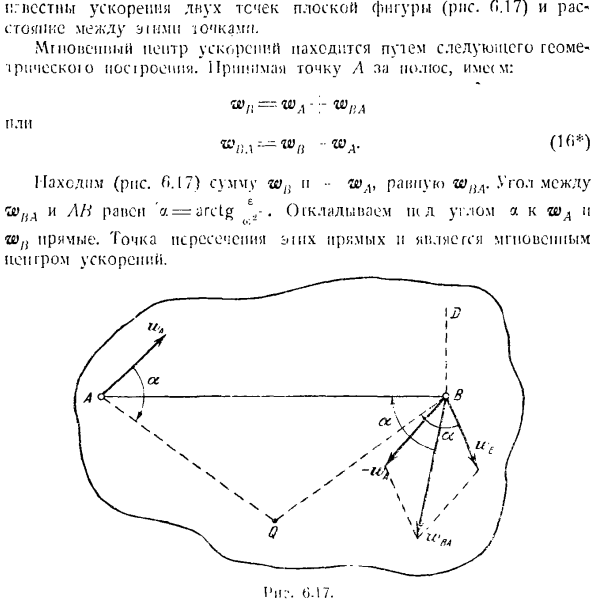
Положение центра мгновенного ускорения, мгновенная угловая скорость и мгновенный угол всех ускорений могут быть найдены в следующих случаях: «В промежутке между плоской фигурой (рис.0.17) утечка летит с ускорением и-это точка быстрого движения. Центр момента ускорения определяется следующим геометрическим сопряжением: принимая точку L 3, J полюсов、 ™Н — ■ ЗО ■ Г и > ИА Или — Западная Австралия. (Привет.) (Рис. 0.17) видно, что суммарные wl $и••wAt равны w / M.
- угол между lfA и an равен a = arctan D -. отложите IU на угол a относительно wA, а wn-прямая линия. Пересечение линий происходит мгновенно Ри:\ (>.17. Определение мгновенной угловой скорости и мгновенного углового ускорения наиболее легко неявно. По этой причине 2-е уравнение (H> *)хорошо разработано для оси HD, перпендикулярной направлению an и AN (рисунок F>.17.): В•= А «4 = Prlv(WLT по) — \ ипали(Уул), с * = |» РВЛ-пр / у(уа). При решении задач экономического развития необходимо их решать. использование ЭИС и т и К и Общ д О-Д и геля с т и Е и Т В и и. A.
рассмотрим 1 точку скорости и ускорения плоской кривой, а также пару правого и левого углов с перпендикулярной осью. О.) Да.) Еще одна точка фигуры Си. Гребная система! Определите точку, в которой ускорение является плоским P n и g. I) найти мгновенный центр скорости, восстановить перпендикулярную линию 1С до скорости 2 точки На планограмме и определить мгновенную угловую скорость ib на рисунке. ’2) определяет центростремительное ускорение 2-й точки вокруг первой точки.
используйте формулу распределения ускорения, чтобы найти ускорение любой точки На виде в плане. Б. Людмила Фирмаль
3) найти значение неизвестного вращательного ускорения из этого уравнения, которое равно сумме проективных всех составляющих ускорения на оси, перпендикулярной направлению ускорения пули, известной. 4) определить мгновенное угловое ускорение плоской фигуры от найденного ускорения вращения. Это дало ускорение в 2 очка от плана этажа.
Надо определить место мгновенных центров осей и осей, а также точек интереса и перспективы. I) рассматриваем первую точку как полюс и проецируем ее на 2-точечную соединительную линию LN. ВТ = 70 — ’ — ПИШЕТ -!-70} » •ШНIИЛIШ / М ’ Найти сумму из полученного равенства, и далее、 Мгновенная угловая скорость плоской фигуры; 3) проецируя то же векторное уравнение в направлении, перпендикулярном/ 1 / Y, можно увидеть величину вращательного ускорения эструса//и, кроме того, мгновенное угловое ускорение плоской фигуры.
4) Найти ускорение любой точки На виде в плане, используя уравнение распределения ускорения. 5) Используйте формулы (12) и (13*), Чтобы найти положение центра мгновенного ускорения. Используя другие известные данные, можно составить подобную серию действий для решения задачи без особых трудностей. Задание 6.19.Цилиндр а упадет и выпьет (рисунок I).Скорость оси цилиндра 1, L = 1 Где Y-расстояние, пройденное центром цилиндра. Радиус цилиндра равен R. Определите ускорение// и положение точки цилиндра Г), С,/Г, / / мгновенно! На разгонном центре цилиндра.
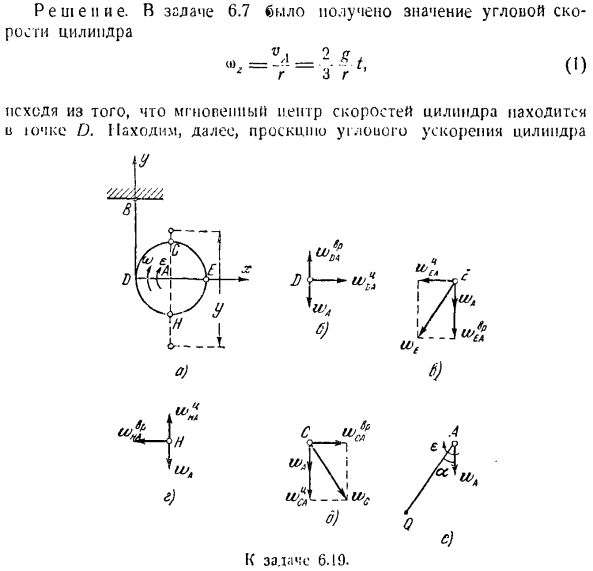
The solution. In задача 6.7, получено значение угловой скорости цилиндра Исходим из того, что центр скорости цилиндра также находится в головке Д. Д. Далее находим проекцию углового ускорения цилиндра. 8р. о.) ИЛ SL. И / Л ТП съел Д. И затем Компьютер. И £4 LL ’ л. О, Боже мой. №. 6р. И в cl Уй. ЮА. е.) т. N И > Л К выпуску 6.19. Как производная проекции угловой скорости времени £ ~ ~ ДТ 3г ’ Перейдем к определению ускорения в точке А. из Формулы(1), оно выглядит так: = = 4
Потому что точка Моти а представляет собой прямую линию вдоль перпендикуляра、 Duright. Или О, нет! = −3 г-(2) Таким образом, вы найдете точку ускорения A. Это единственная точка цилиндра, и ее ускорение известно, поэтому его следует считать полюсом. Приступайте немедленно к определению ускорения! О центре скорости цилиндра-точка/). но часть D ускорения представляет собой геометрическую геометрию из 3 ускорений:
IO / носовое ускорение, центр колымаги poio, при вращении фигуры и вокруг полюса (рисунок B): 1л)=— Д М а-ЛВД < \ » — * ч) л ’ Ускорение полюсов направлена вдоль Р » Эпи икали shhz. П. А. Ойсладивасм 3101 горное утверждение от Ю. Например, ускорение вращения точки L) и окружающих ее полюсов Угловая скорость и угол> tsplnndra форма дуги стрелка направлена в сторону Стрелки C1.Это получается из рассмотрения скорости точки А как скорости вращения вокруг мгновенной пещеры высокой скорости D.
As в результате ускорение вращения направляется вокруг гайки D, но не записывается bv ^ px. Эти 2 составляющие величины=и, следовательно, ускорение точки D стирает гомосексуалистов друг с другом. Цсшршпрщшейюююй ици рение точек д вокруг А, но значение есть Эхо-ускорение направлено от оси D к состоянию L. таким образом, абсолютное ускорение оси D устойчиво, но относительно ускорителя-модуля ускорения.
Неподвижный цилиндр представляет собой прямой цилиндр, окружность которого соединена с осью времени центром мгновенной скорости, отмеченным на неподвижной плоскости. Движущийся цилиндр центра тяжести-окружность Cl: h’D. следовательно, мгновенная скорость центра ускорения пятна D направлена вдоль нормали неподвижной цепи и подвижной цепи Ллойда. Если вы получаете точку D, как и раньше, она выглядит так на полюсе (рисунок C). Значение ускорения w ^равно значению w * A(4).
в этом случае это ускорение представляет собой нанопреобразование от точки E до полюса L. значение имеет направление w»?Равны размеру ^и перпендикулярны к ^ К и wv как Калия. Таким образом, величина ускорения точки/; wK = = U V 1 Направление мы » формула: = = —- 。 ^ ВЧГ.- ^Я потому что(A -, в)= = —— = ——• л / л• Определите точку / y ускорения (рисунок D): ^ // ^^-«’//。ГГ^- Направление ускорения составляющей точки и показано на рисунке. г, их значения известны. Они есть、(2)、(3)、(4)оно трактуется так же, как и выражение. Значение ускорения точки II ■ : — =хй \ л «1• Направление ускорения определяется по формуле:
Проекция ускорения движущейся координатной оси с точкой M определяется по формуле гей. wxi -» ’ o,*,—(3 *) «L = + -» h’i-(4 *) В этих уравнениях g,,, является проекцией ускорения точки Подвижная ось x tt tt * 0, JC1, V1-проекция ускорения полюса O, подвижная ось x1, X1, y2-координаты точки M подвижной оси. u> z-уравнение (1), (!2) и то же самое. / УФ / ВМ ТШ. В // потому что (ш / Р)= -= Y / Аналогично(Рисунок E) ! / Определите положение мгновенного центра ускорения. Угол, составленный по направлению к центру мгновенного ускорения при ускорении любой точки в плане,
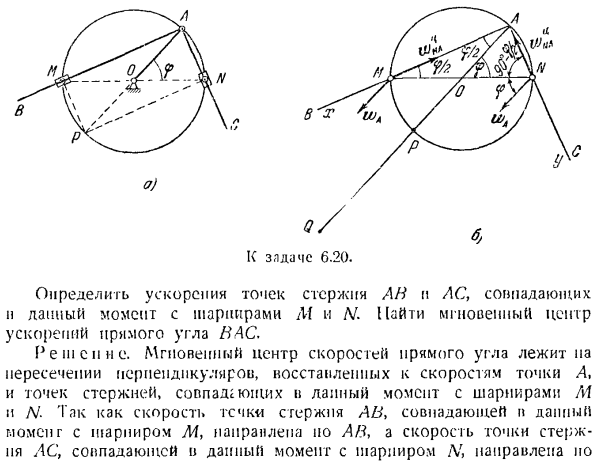
определяется по формуле Расстояние от точки А до мгновенного центра ускорения Q г. Отложите угол i от направления ускорения точки А до направления дуги е, то есть по часовой стрелке. Эта папирусопатия откладывает отрезок AQ от точки A. конечная точка точки A является центром мгновенного ускорения. Задание 6.20. Точные прямые углы BAC (Рис.1) перемещаются так, что стержни AB и AC проходят через неподвижные точки M и / V, которые находятся на окружности, движущейся с постоянной скоростью V, при которой вершины вращаются за счет ползучести OA.
Радиус окружности () A-j = i \ Теперь определим ускорение стержня точками AH и AU, которые совпадают с шарнирами Af и N. найдем центр ускорения прямого угла AS. Решение. Центром мгновенной скорости прямого угла является point. At точка пересечения перпендикуляра, которая восстанавливается до скорости 4, и точка стержня, которая в данный момент совпадает с шарнирами M и yv. Скорость стержня переменного тока, которая в данный момент совпадает с шарниром шарнира, ориентирована вдоль AB, а скорость точки стержня переменного тока, которая в данный момент совпадает с шарниром L’, ориентирована вдоль него.
Как, то центр мгновенной скорости находится в точке P, угловая скорость момента трассировки и телпо, прямой угол V V = = COHSt. В результате мгновенное угловое ускорение прямого угла равно пуле. Ускорение стержня в точке wM, которая в данный момент совпадает с шарниром шарнира/, состоит из 3 ускорений. =™Л НГ » фут * + Где W-ускорение полюса в точке А. Это единственная точка, в которой ускорение прямым углом известно. —
Центростремительное ускорение; zd ^ p — ускорение вращения точки A1 вокруг полюса. Найти эти ускорения: величина полярного ускорения В * / Я \ уа = г (я) Это ускорение направлено из точки А В точку О.- Равное ускорение К, = я■<т-2г ■ СОА г ■ тг°= 2г■C0S 2 И она направлена от точки М к полюсу, к точке/ 1.Ускорение вращения = AM = 0. Отложим эти составляющие ускорения от точки М. выберем координатные оси (рисунок Б), но найдем проекцию ускорения точки М на эти оси со стороны прямого угла. ф В — О В-О В-О = ш ^ соз%-= 7 Кос-■—^ .потому что — * = ВР соѕ х、 Сайт WMX. О ХК. © «\ЦУ Силл ^ = 7 Ши-Дж.
Следовательно, коэффициент ускорения точки L1 Направление ускорения следует определять по формуле гея. Да.. потому что. потому что(вм, х)=—;-•• 1 / u:-3sirie’t _ > грех ’ / ч ^ т ’ в cos («m. y)= … Дж / я-J-3 грех — -.y- «Я.•/- ..? Приступайте к принятию решения. Шарнир A ’ и точечное ускорение согласующего стержня: ЗК.- =Вайоминг — \ — з%, Т. Л, Л, Л, Л, Л, Л, Л, Л, Л, Л Ускорение полюса wl определяется по Формуле (1).Отложите от точки A ’(рисунок B). поскольку evr = 0, ускорение вращения равно нулю.
Найти величину центростремительного ускорения от точки А до полюса и точки А. к.. л = лы-2р подоконник * ^ — 5 грех Далее определим проекцию ускорения wr pa на естественную малую координату. С тобой ^ л- ^ соз * — р потому что я、 про А3. о.2.о У2.О WXy = WA sin — ™% n = y L1n-L> — SHI v = 2-SHI Используйте эти формулы для определения модуля и направления ускорения wx. ) 1-; ч»»•**. .1? потому что (Вайоминг, х)= -=- * J Я -; — 3С («С2 Вт грехом, г потерь J’) = =—— *) я. ;- 3cosj — ®
Центр мгновенного ускорения Q. тг»=::; = о、 мг. Итак, мгновенный центр ускорения Q находится на прямой, проходящей через точки O и L. расстояние от точки A до мгновенного центра ускорения Q Так, центр мгновенного ускорения расположен на расстоянии 2 диаметров точки А или 1 диаметра от мгновенного центра R скорости. Задача 6.21.Плоский прямоугольник движения LPSO. Ускорение точки А в данный момент? И r равно wA — = 2 см / сек1、 Так… Л. Так… Один. Задач г. до 2И. Сделайте все линии и углы 30°.
Ускорение точки B составляет wn = =-0 см / sat * 4, образуя угол (прямая линия / ZA и DOL. Длина сторон: AB = 10 см, HC = 5 см. *) Определите угловую скорость прямоугольника и мгновенное угловое ускорение, а также ускорение точки С. Решение. Выберите точку полюса A. Затем ускорение эструса B н. составьте векторное уравнение(1) по осям x и y (см. рисунок). если вы проецируете его на ось x, он выглядит так: -wB cos GO0 = — wA cos 30° — zrj Откуда? wl} fA = wA cos 30° — (- wJ {cos 60°x 4,73 см / с \
Здесь мы находим мгновенную угловую скорость фигуры если вы проецируете векторное равенство (I) на ось y, оно выглядит следующим образом: — wDcos 30°= уа грех 30°-з * ф> А. Отсюда определяется ускорение вращения точки B. = wDA cos 30° — f wA sin 30°6.19 см / с *. Затем найдите мгновенное угловое ускорение фигуры гиг=!що, б19 секунд.-\ Угловое ускорение фигуры направлено вдоль оси z в отрицательном направлении. Определите ускорение точки C.
Выберите точку B на полюсе и следуйте уравнению для распределения ускорения, как показано на рисунке Tf. = + ВАК-Р Если мы спроецируем это уравнение на оси jt и y, то увидим, что: расширением WCX = — ч соѕ(10°-wjfc ^-6.095 КМУ ск4、 туалет = — wBcos 30° — п з » с б-2.825 см, ЧСК *. Теперь вы можете легко найти значение ускорения точки С. wc = V 45 6,7 см; сек*. направление wc определяется по формуле: потому что(душевая кабина, туалет> х)= 0.906、
Величина ускорения точки м от известной проекции равна уравнению ^ =- 3Г = / я ^ JTij-Т: (5 *) Гид коссейн в равной степени: потому что(СГ, С»)=^, потому что(ж, г)= (Б *) — Х Вт V / ^ ы ш потому что(ж, ху)=, потому что Джей каши)=. (7 *) У ’ 1ч / Метод графического анализа. Первый метод графического анализа для нахождения ускорения точки На плоской фигуре основан на выражении распределения ускорения (рисунок В этом уравнении wAl — общее ускорение в любой точке 11 на виде в плане. wn-ускорение полюса O. W \ { / ) — центростремительное
потому что(ж ^ г)= = −0.422 Задача 6. 22.Параллелограмм апута образован стержнем: AD = BE = 10 см и AB = ED = — см、 1 ′ 3 Соединенные шарниры(рисунок I).Звено АБ неподвижно. Угловая скорость его штока равна. до 22. Если мысленно соединить точки B и D линии, то Треугольник ADB и BOE будет равен 3 равным sides. As в результате,/ DAB = Z. кровать и LABE = / _ El) A. тогда треугольники AP B и EPD равны и имеют равные стороны AB = ED и равные углы. А потом, конечно, Итак, в условиях данной задачи сумма расстояний от мгновенного центра скорости стержня ED до 2 неподвижных точек a p B ecib является постоянной величиной. Резьбовой стержень 6.)
PB = PD Терио Р Плоскость дилатации печени представляет собой эллипс, фокусом которого являются точки A и B. Этот эллипс является фиксированной центральной точкой. Из-за особенностей эллипса Нормаль эллипса в точке является биссектрисой внутреннего угла между фокусными радиусами, то есть биссектрисой угла ARV. So, ускорение точки Р направлено вдоль биссектрисы угла ARV.
In в этом случае мгновенная скорость центра стержня EJJ не должна смешиваться с точкой P, принадлежащей стержню BE. Ускорение в этой точке состоит из 3 ускорений: ускорение полюса, центростремительное ускорение вокруг полюса и вращательное ускорение. WР = мы + Е * Ж *?Е. (2) 3 (рис. 1) эти ускорения. Ускорение 40 см / sccK откладывается от точки P вдоль стержня EB. w’) для определения.
Во-первых, определить мгновенную угловую скорость стержня Эд. Если считать, что точка е принадлежит стержням BE и стержням ED, то: вэ = ц0-быть — * ЕР、 Откуда? Да. Шмг = ш0 «= 2•20•3 = 3 ФФК В этой формуле А! — Тит-Кара-2ад-3 СЛГ、 Вытекало из условий / s7> P [) = AP — \ — PB = AD = 10 c. из w и уравнения (треугольник / iD / 5-прямоугольник) Здесь мы определяем центростремительное ускорение точки P. ш » Ф = ЕР•ИГ; Р=. 9 = 60 см {s . Это ускорение направлено от точки P к полюсу в точке E. ускорение вращения wjj.
Угол APB, как видно из рассмотрения треугольника APB, равен 60°, поэтому ускорение точки P равно углу P = 30°с линией PB. Если проецировать равенство векторов (2) в направлении, перпендикулярном wP, то мы увидим, что: 0 = 40 cos 60°-60 cos 60°+ cos30e、 Так… вффи? 20 3 / г евро -=• — — -. , 4rv — = y 3 секунды\ mg-RE-узлы 20 Рассмотрим экологию углов и определение углового ускорения стержня AD. To для этого определите ускорение точки D, которая принадлежит одновременно стержню ED и AD(рисунок C).
Ускорение точки D, принадлежащей стержню ED, представлено следующим образом: Компания WD = мы-rWDE + получите самые яркие впечатления(3) Ускорение направлено из точки D в точку E, его модуль = Де ж » Ф =〜. 9 = 30] / 3 С. I / s*. В. Откуда? 20 0.5-2 20 2, ГФ-кг•=-^-= —7-。 смккк. Ре U з узел Ускорение направлено перпендикулярно Φ\Γ и его модулю. = = ’V * = 10 см’ ssk *. J ’ 3. Он известен своим размером силы ускорения (1) и направлением. Поэтому во всех точках 1) определяются 3 составляющие ускорения.
С другой стороны, если стержень вращается вокруг неподвижного центра, Точка I)рисует круг. Если проецировать (3) на нормальное AD, то найдем абсолютное нормальное ускорение точки I. = в COS(10° — интерфейс’1 ^ = −40-0.5-10 = 10 см; УП \ Тогда как? == <0j./У)、 Где o) — искомая угловая скорость стержня AD. — Я / ю-/»- Проецируем уравнение(3) на касательную к траектории точки D. [: На прямой D находим абсолютное касательное ускорение точки D w’h = wlR-cos 30°= 30 V3— = 101 / s или позже ав.,£== ЛО.、
Где] — желаемое угловое ускорение стержня LD. WD U / 3 Таким образом, видно, что регистрируется угловое и угловое ускорение всех вершин параллелограмма ВНП, что позволяет определить скорость и ускорение любой точки на механизме. Затем определите положение центра мгновенного ускорения стержня (ГГ).Вычислите угол между ускорением любой точки стержня ED и направлением ускорения Q к мгновенному центру. мг. Найти расстояние от точки P до центра мгновенного ускорения Ч. Мы вэлью. В7 Особенности:= = -: — = 4.37 см.
В 3-х моментах ускорение Р откладывают от направления IID, совпадающего с ускорением точки E, а затем рисуют пастбищную стрелку emg угла поворота направления a (рисунок C) и отрезок EQ длиной 4,37 см. Задача 6.23.Коленчатый вал OA = r = 10 см вращается вокруг неподвижного рыскания O по формуле
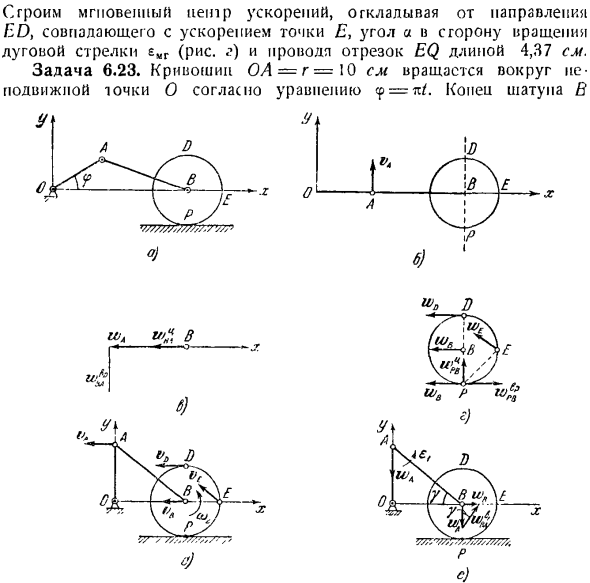
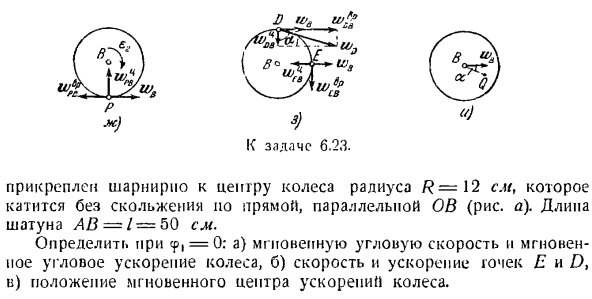
4. д. * ^ ?.> ч «У» П-твэп л• ’ Си、 А, к Задача 6.23. Шарниры крепятся к центру колеса с радиусом R-12 см и вращаются без скольжения по прямой, параллельной Обь(рисунок а).Длина стержня AB = / = 50 см. определить новую угловую скорость и мгновенное угловое ускорение колеса mg, б) скорость и ускорение точек E и D, а) положение центра мгновенного ускорения колеса, при < p,= 0. Решение. Рассмотрим начальное положение механизма-O (рисунок B).Выберите фиксированную систему координат, началом координат которой является точка O.
ось l*направлена вправо, ось OB направлена вправо, ось y направлена вверх и перпендикулярна оси l, а ось z перпендикулярна плоскости перемещения. Проекция кривошины кривошины оси pa z о> 2 = ^ = я сек ’ 1. Значение скорости точки А va = OA — / j = I Augg см / с, (1) Кроме того, эта скорость направлена перпендикулярно кривошипу OA(рисунок b). Чтобы найти мгновенный центр скорости шатуна, вам нужно знать направление его 2 точки скорости.
Первая точка, в которой известна скорость, — это A, которая принадлежит кривошипу и Шатуну.2-я точка шатуна с направлением скорости известна-это точка B. In дело в том, что точка B движется линейно вдоль оси x, и поэтому ее скорость также направлена вдоль этой прямой. Мгновенный центр скорости шатуна LV находится на пересечении перпендикулярных линий, восстановленных до скоростей точек L и B. перпендикуляром к vA является AB, а перпендикуляром к vn-линия DP(рисунок B).
Эти перпендикуляры пересекаются в точке B. So, точка B в этом положении механизма является мгновенным центром скорости стержня AB, а скорость точки B равна скорости пули. Определите мгновенную угловую скорость колеса. Точка B принадлежит колесу, его скорость равна нулю. Точка P является мгновенным центром скорости вращения колеса, которое представляет собой горизонтальную линию, но не скользит.
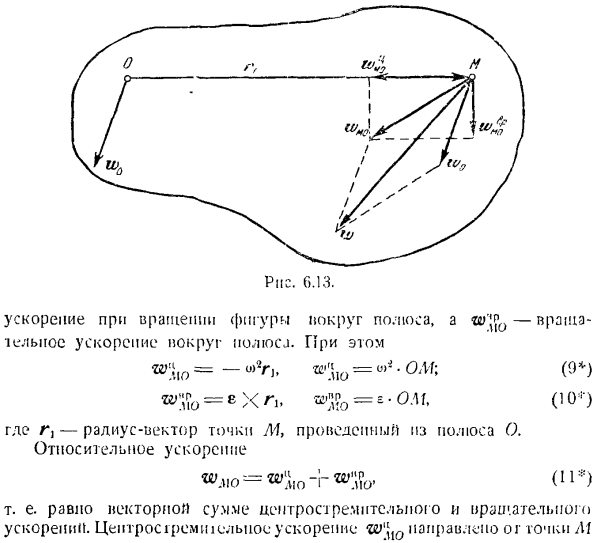
Таким образом, скорость точки P равна нулю. Поэтому в данный момент мгновенная угловая скорость колеса равна нулю, а скорость всех точек колеса равна Ускорение при вращении фигуры вокруг полюса, а w ’ § 0-ускорение вращения вокруг pole. At в то же время Ж%0 =-0> В,, Ш ’ \ п0 = о> 3 * ом; (9 *) и> 7y = 8П,,®3f0= ^ * OLT. (10-) Где r-радиус-вектор точек в UI, взятых из полюса O. Oti. *> МО * = *> {п0-Р *> \ ИФО- <Н *) Другими словами, центростремительное ускорение и ускорение вращения равны сумме векторов.
Ускорение цепи, w \ 0, центрируется в точке M Конечно, нуль =ЩXП、 Где * = 10 см ’ сек Аль-Зи. / Поскольку это нормальное ускорение, оно направляет ва из точки А В точку О… •(3) Куда? И.«= ПА•СШ = 50•ГУ = см-Е К’1. Ил я; Г Ускорение w’jn направлено от точки B к полюсу и к точке A. отложите компоненты w ^и W} iA ускорения точки B в выбранном maeppub(рисунок P). 3-й компонент w * gA направлен перпендикулярно WfiA и меньше по размеру.
Сумма 3 векторов по (3) должна быть равна wn. Однако точка B движется линейно вдоль оси x, поэтому ее ускорение должно быть сделано вдоль этой оси. если проецировать равенство (3) на ось y, то получим: k»»} d = 0, то есть e,= 0, а ускорение точки B направлено от B к точке A. если проецировать уравнение (3) на ось x、 ој = — з-. =- I от: ’1-2-1 = — 12ит1 см сек *. / N л ал ал я
Точка B должна быть выбрана на полюсе как единственное колесо cc, которое одновременно принадлежит колесу r и ускорение известно. Мгновенное угловое ускорение колеса неизвестно, поэтому сначала нужно искать ускорение точки, если ускорение известно в этом направлении. Такая точка есть только в период течки. Его ускорение представляет собой тангенциальное ускорение, которое направлено вдоль нормальной линии центра тяжести, то есть от точки Р
К центру колеса в(рисунок D). Мы ищем ускорение точки P по уравнению распределения ускорения. ч = ЗП-Р wHnJrwBA(4) Отложим направление этих 3 составляющих максимального ускорения от точки P: WFI и направлено по касательной к центру тяжести-вертикали, максимальное ускорение wp направлено вдоль PB. если вы проецируете уравнение (4) на ось xy, вы знаете: О = (о) Таким образом, компоненты wB и wyn направлены в разные стороны и имеют одинаковую величину.
Подставляя эти значения в (5), он выглядит так: 12? = ВР * е.»、 Откуда? £ — 2 — = = секунды* (£j, глядя из направления, параллельного против часовой стрелки Стрелка.) С другой стороны, если спроецировать (4) на ось y, то можно увидеть следующее: WР = W} в = ВР -** = о、 Потому что мгновенная угловая скорость колеса теперь равна пуле(2).Таким образом, мгновенный центр I и мгновенный центр ускорения колеса при этом положении механизма совпадают и находятся в точке P. Точки C и D остаются для определения ускорения.
Они равны ж, — = £iXrE> Где rE-эстральный радиус-вектор E, взятый из мгновенного центра ускорения P \ rD. Аналогичный радиус-вектор в точке L. модуль этих ускорений выглядит следующим образом: we=µcv ’ 2 = V2 * 12-2 см; sec \ wD = .2R = 24 см ’ сек. Направление этих ускорений определяется по правилам векторного произведения и показано на рисунке. г. Задача 6.24.Решить предыдущие проблемы с расположением механизма Угол<Р * =
Примечание: скорость точки A равна по величине (см. Рисунок E) ва = АО•; <о! = 10 * см; секунды И она направлена перпендикулярно к / 10.Скорость точки B параллельна скорости точки A, потому что точка B движется вдоль оси jc. если мы восстановим перпендикуляры VA и vlP, то придем к выводу, что они не пересекаются. Поэтому в данный момент шатун мгновенно движется вперед, и скорости всех его точек равны между собой, особенно ВБ = ва、 И в этот момент угловая скорость<0j равна нулю
. Точка B, с другой стороны, принадлежит колесу, где центр мгновенной скорости находится в точке R. поэтому、 Где-мгновенная угловая скорость колеса? Отсюда ВЛИ Юп _ | У меня есть секунда Найти скорость утечки/; it D ВД = у Х ГП Следовательно、 vn = u) r = 14,1 tf см / с,= o. = 20tg см ’ сек. Направление этих скоростей определяется по правилам векторного произведения и показано на рисунке. д. Переходим к определению ускорения.
Определяется величина ускорения точки А. Это ускорение направлено от А К О (рисунок е).Ускорение точки B получается выражением распределения ускорения, а на полюсе получаем точку A, которая принадлежит Шатуну. ВБ — = уа + ка +™7А это’о Из точки B проведите прямую линию в направлении, перпендикулярном Шатуну AB, который соединяет полюс A с точкой B. Компонент= so ka, угловая скорость o>、 В этом положении она равна нулю. С другой стороны, ВБ направлен вдоль Оби. Если мы пойдем прямо из B в направлении O B, мы найдем точку пересечения этого ripni и направления. w 11 и w ’;?Один.-
Если мы обозначим угол OVA через y и скажем: «обратите внимание, что угол между m и этим углом поврежден, мы видим, что: * ОА Ю ЛОЛ. тг т = т = …..__ = = 0.204 &1 OB yTfQ * _ 1Q2 Если проецировать равенство (1) на оси, то оно выглядит так: В11 = Ш «?А грех б 0 = WHjPA COS y-WA. Если мы решим эти уравнения вместе, мы увидим, что: ЗП = ва Тан 1 = 1 О * ’ 2. 0.204 = 2.04 к * elfek \ ЗКО В и — в * = — в «п0 — Р 2.04 — = = 10.2 * * ы Величина углового ускорения шатуна lb в этом положении、 £ , = = — Круто— = 0.204 Л1 с ’1 ли ОО
Поскольку мгновенная угловая скорость момента шатуна равна нулю, вращение шатуна ускоряется. Определите ускорение точки колеса. Точка B должна быть выбрана на полюсе. Это потому, что это единственная точка на колесе, где ускорение известно. Затем найдите ускорение точки P, которая является центром мгновенной скорости. Это потому, что это единственная точка на колесе (за исключением P, которая приобретается полюсом).Согласно теореме распределения ускорения «/>=»И+(2)
Ускорение точки Р, совпадающее с мгновенным центром скорости, направлено перпендикулярно центру gravity. In в этом случае неподвижный / 1 цент корпуса представляет собой прямую линию, но если колесо вращается, то подвижным центром тяжести является обод wheel. As в результате wP направляется на RV. Отложите WB от точки P (рисунок G). Wj направлен на одну и ту же прямую линию, а размер неизвестен. wxfiJi направлен от Rp к V. Если проецировать » равенство (2)» в направлении BP, то это выглядит так: 1 lg-2 WР = *%= Р•^ = 12• — = \ см \сек(3)
Если проецировать уравнение(2)в направлении, перпендикулярном BP, то оно выглядит так: Wu = = 2,04 К2 см / с *. (4) Затем найдите значение углового ускорения колеса Стрелка на Стрелке c (рисунок G) должна быть направлена Clockwise. As в результате вращение колеса замедляется. Ускорение точек D и P выражается формулой
вайн и ко. Формула(3) и(-!Как вы можете видеть из;, их значения w, j, n и Знак ускорения wn и w {;. ЗП = VWT ^ дя* — = = 9.25 т: * см / ССК-、 Вт= ,/ = г(8.33—2.04 Т:») » — Джей — (2. 04n2) * = 0.0 Т:2 см S Определите угол a, который складывается из ускорения точки и направления полюса B. о точках [) — Я… — Эд, — я… ОСР.- О точках/; тг А2.= ——- = = 0.32 примерно. РГ.»«»Эта организация」 Отсюда и ускорение точки/.) И Z: ’найдено по размеру и направлению.
Далее определите положение центра мгновенного ускорения колеса. Найти угол a, определяемый уравнением 。 £.. 0.17-Н *. 12 * Lo41 Откуда? И 13 40 ′. Против полюсов O. ускорение вращения направлено перпендикулярно. Это направление вращения плоской фигуры, если вращение ускорено, а если вращение медленное, то в противоположном направлении, параллельном радиус-вектору gx. Таким образом, чтобы определить ускорение любой точки M, необходимо, чтобы ускорение точки полярного планетоида, мгновенная угловая скорость планетоида и, наконец, e было мгновенным угловым ускорением.
Затем, суммируя 3 вектора w0> w [\ UJ, (рис. 6.13), получаем искомое Ускорение точки M как сумма этих векторов. Это решение может быть применено, когда угол поворота плоскости фиг. 9 является известной функцией. Это связано с тем, что вы можете определить ez, вычисляя производные 1-го и 2-го порядка угла поворота по времени. Во многих задачах зависимость угловой скорости от времени неизвестна. Мгновенная угловая скорость 1 A Воскликните 6.25. Точки равны («>mg = 0).Скорость точки А, а значит и скорость любой точки На шатуне vA = OA-to ()= 20 см / с
Ускорение в точке А представляет собой сумму нормального ускорения с равными значениями и тангенциального ускорения wnA =ИО * u > J = 20 см / сек\ w’A = AO•e0 = 20 * 0.2 t: = cm’SEC. Выберите точку A на полюсе в качестве единственной точки шатуна, в которой известно ускорение, и примените формулу распределения ускорения в точке B ™Б =™Айр в> Ла-Д О) В этом случае WF {величина и направление неизвестны, а величина неизвестна. Поэтому невозможно найти искомое количество непосредственно из Формулы (I).Воспользуемся тем, что можно определить нормальное ускорение точки B в%(20р) 2 40 ®3= d = T (G = T77 см1 сек-
Если проецировать уравнение (1) на Нормаль, то есть на вертикальную ось траектории движения точки Wu, получим: wnn = wnA -sinsin Y-W * ga COS 7, (2) Где Син-ы= ^ = 0.5; 7 = 30°。Найти значение ускорения по формуле(2) ВАЗ-уютно — / / с 3 Дж / 3 » = = AB » потому что это co2, r = 0 (рисунок b).Следовательно, величина углового ускорения Да. в ЭМГ = — ^ = 0. 192tg2 второй R направлен против часовой стрелки по знаку w * fA * £mg. Найти касательное ускорение точки B и спроецировать равенство (1) на OB. wzH = w ’A-sin 7 == 4:: — 7-tg — *’ =-25,4 см / с *. 3 года 3 Размер точки ускорения B wn = +(u)* = 135 см / с *. Угол, состоящий из этого ускорения и прямой 0 \ B, определяется из уравнения ™Б _ 25.4
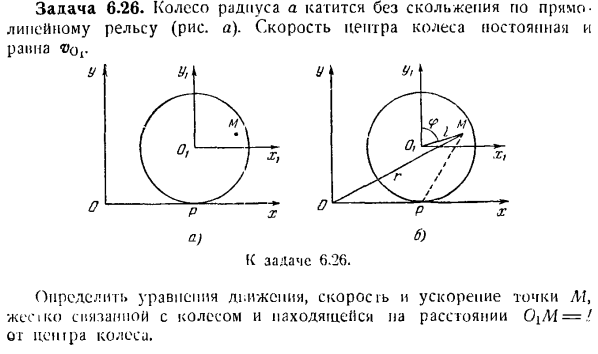
Задача 6.26.Колесо с радиусом а катится без скольжения по прямой линии рельсов(рисунок а).Скорость центра колеса постоянна、 а) 6) Задание 6.26 к. Соединенный с колесом, расстояние 0 {M = /.Определите уравнение движения, скорости и ускорения точки М в точке В. Из центра колеса. Решение. Выберите фиксированную систему координат xy и подвижную систему координат X \ yx. Движущаяся система координат постепенно перемещается вместе с центром колеса, а ее ось остается параллельной оси неподвижной системы. Величина угловой скорости колеса определяется из уравнения(рисунок Б)\ по качеству звука 1 = Р01-о)= ах
Потому что центр мгновенной скорости находится в точке контакта P колеса и неподвижного rail. So … О (1) умножьте pa dt и рассмотрите его У нас есть: Но… При интеграции вы увидите следующее: (2) Верите ли вы, что? — О, для f=, из(2), Любой интегральный Интеграл равен Ci = 0, а в конце、 Координата точки M и система координат перемещения: ВГ. Х \ = Я Грех = / Грех-л-т、 Но… ВН. Йи = я, потому что 9 = / потому что Т Координатами точки A1 в фиксированной системе координат являются координаты начальной точки движущейся системы 0Jt и сумма координат (3). ВН. х = x0l-+ — ХL = V0lt-\ — л грех Т、
Радиус-вектор в точке M в фиксированной системе координат выглядит следующим образом: r = [v0lt + / tin » * f)i +(a + / cos / J y, i, Y-ось координатных осей. Скорость точки Af определяется как производная по времени от радиус-вектора // вн вн !ВН. ВН. В = iv0l -!- потому что —0л-грех Т./ \ «А (а) (а)» Скорость точки A / ориентирована перпендикулярно мгновенному радиусу PM.
Ускорение точки M CCI производная скорости во времени (4) Вт= -?? «(СЛН ^ »» + что-SiIj). (.- О, rhpus-pekgor 0 {м РЛ = OlAt = Xll-модуля-trylJ = л [грех объекты первого класса ^ в)、 Представим себе форму ускорения(4) ж = — — — ^ р、 Г.-* Таким образом, ускорение точки A1 является величиной, а направление точки M постоянно по направлению к центру колеса. Задача 6. 27.Прямые стержни AB выполняют плоское движение. Ускорение ziaya точек A и B определяет точку C линии AB.
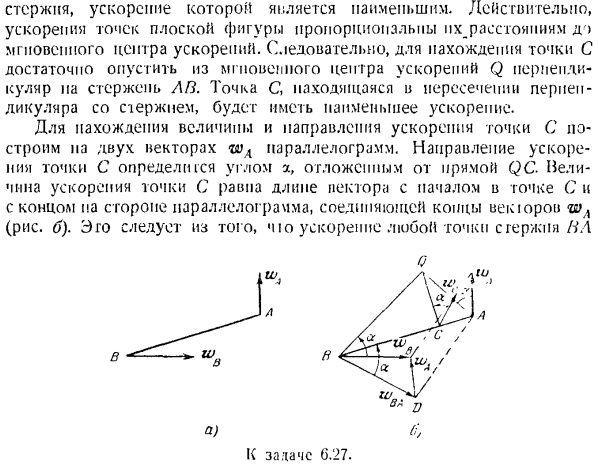
Ускорение линии АВ минимально, а также определяет величину и направление ее ускорения. Решение. Метод графического анализа. Если рассматривать точку А как полюс, то используя формулу (H4 -) находим: = ва 4- ™ ба -!- w7A = wA + ™ » Л> Размер и направление По этой причине мы откладываем ускорение wu и рассольную сумму wDA-j-WA из точки B (рисунок B).Ускорение wDA образует первичный B A и угол a.
Если вы знаете угол a, вы можете увидеть центр мгновенного ускорения стержня. Поэтому отложите ускорение wA и угол a от wn в том же направлении, в котором прямая BA смещена от wBA. Точки пересечения линий BQ и AQ определяют положение центра Q мгновенного ускорения. Если знать положение центра мгновенного ускорения, то можно легко найти точку С. Стержень с минимумом acceleration. In дело в том, что ускорение точек в плане пропорционально расстоянию до мгновенного центра ускорения. Поэтому, чтобы найти точку C, достаточно опустить из центра мгновенное ускорение Q перпендикулярно плоскости PL Rod.
At в точке С на пересечении перпендикуляра и стержня ускорение минимально. Чтобы найти величину и направление ускорения точки C, создайте 2 вектора параллелограмма, wA, на 2 вектора. Направление ускорения в точке C определяется углом a, отклоненным от прямой QC. Ускорение в точке с начинается в точке С и равно длине вектора в конце параллелограмма, соединяющего конец wA века (рисунок B).Эго вытекает из ускорения любой точки стержня Ил Да.
адаче 6.27. Далее производится по формуле (8*). 1 из точек плана этажа, по которым можно определить направление ускорения, совпадают с мгновенным центром скорости. Ускорение в этой точке является тангенциальным ускорением. В.- поскольку v равно O, ускорение пормальпического wn-становится равным нулю. Ускорение собственного веса направлено вдоль общих нормалей неподвижной и движущейся технологической лопасти. Давайте рассмотрим пример. Давайте нарисуем его на схеме.0.14 колесо Ка-1 и транспортное средство не скользят по rails
. In в этом случае обод колеса является подвижным центром тяжести, а рельс неподвижным. Ускорение точки колеса с направлено перпендикулярно центру тяжести, то есть к центру колеса О. На рисунке показан сегмент циклоиды, являющийся локусом в точке С. Конечно, ускорение Wc направлено по касательной. Сумма относительного ускорения, параллельного waA, пропорциональна расстоянию точки до полюса A и ускорению полюса wA. Конечная точка относительного ускорения любой точки стержня находится на линии DA.
In помимо ускорения полюсов wA, мы можем видеть, что конец ускорения любой точки стержня AB лежит на стороне параллелограмма, соединяющего конец вектора wA. Значение ускорения wc можно найти другим способом. Я заметила. ОС * 1 ОС У нас есть: КК =ила Вт » в- Для того чтобы овладеть навыками решения задач в конкретных точках ускорения, мы легко решим и решим следующие задачи из»сборника задач теоретической механики». Я… В. Мещерского, издание с 1950 года
Сумма относительного ускорения, параллельного waA, пропорциональна расстоянию точки до полюса A и ускорению полюса wA. Конечная точка относительного ускорения любой точки стержня находится на линии DA. In помимо ускорения полюсов wA, мы можем видеть, что конец ускорения любой точки стержня AB лежит на стороне параллелограмма, соединяющего конец вектора wA. Значение ускорения wc можно найти другим способом. Я заметила. ОС * 1 ОС У нас есть: КК =ила Вт » в- Чтобы овладеть навыками решения задач в конкретных точках ускорения, Л И Л И К и Ф и Гурий очень хорошо решают очередную задачу из»сборника задач теоретической механики». Я… В. Мещерского, издания с 1950 года: 557
, 5Г4、565、508、569、572、575、578。 Решение некоторых задач определяется определением ускорения точки На плоской фигуре. Это происходит потому, что нормальное ускорение плоской точки может быть известно. Тогда задача устроена следующим образом: 1 точка ускорения плоской фигуры-полюс O, величина мгновенной угловой скорости фигуры (o, кроме того, задается обычное ускорение любой точки M).И получаем уравнение, которое определяется из 1 неизвестного a> JJo». оно вычисляет мгновенное угловое ускорение r, зная w \ f0
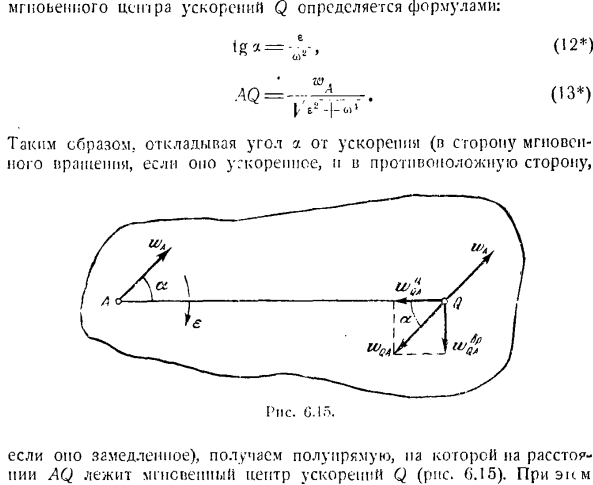
Кроме того, используйте формулу распределения ускорения(8), чтобы найти ускорение любой точки На виде в плане. Одним из широко применяемых методов графического анализа для определения ускорения точки На плоской фигуре является использование понятия центра мгновенного ускорения. Мгновенный центр ускорения — это точка в плане этажа, где ускорение теперь равно нулю. Позиция Мгновенный центр ускорения Q определяется следующим уравнением: (12) (13 *) с. .4кв =-•; — И ’ — / s»
Таким образом, отложите угол a или ускорение(в направлении мгновенного вращения, если n противоположно, в противоположном направлении, n Инжир. 15. Замедление), получим полулинию, где имеется мгновенный центр ускорения Q на расстоянии i4Q(рисунок (>.15)).
Сумма относительного ускорения, параллельного waA, пропорциональна расстоянию точки до полюса A и ускорению полюса wA. Конечная точка относительного ускорения любой точки стержня находится на линии DA. In помимо ускорения полюсов wA, мы можем видеть, что конец ускорения любой точки стержня AB лежит на стороне параллелограмма, соединяющего конец вектора wA. Значение ускорения wc можно найти другим способом. Я заметила. ОС * 1 ОС У нас есть: КК =ила Вт » в-
Чтобы овладеть навыками решения задач в конкретных точках ускорения, Л И Л И К и Ф и Гурий очень хорошо решают очередную задачу из»сборника задач теоретической механики». Я… В. Мещерского, издания с 1950 года: 557, 5Г4、565、508、569、572、575、578。 Решение некоторых задач определяется определением ускорения точки На плоской фигуре. Это происходит потому, что нормальное ускорение плоской точки может быть известно. Тогда задача устроена следующим образом: 1 точка ускорения плоской фигуры-полюс O, величина мгновенной угловой скорости фигуры (o, кроме того, задается обычное ускорение любой точки M).
И получаем уравнение, которое определяется из 1 неизвестного a> JJo». оно вычисляет мгновенное угловое ускорение r, зная w \ f0 Кроме того, используйте формулу распределения ускорения(8), чтобы найти ускорение любой точки На виде в плане. Одним из широко применяемых методов графического анализа для определения ускорения точки На плоской фигуре является использование понятия центра мгновенного ускорения. Мгновенный центр ускорения — это точка в плане этажа, где ускорение теперь равно нулю.
Позиция Мгновенный центр ускорения Q определяется следующим уравнением: (12) (13 *) с. .4кв =-•; — И ’ — / s» Таким образом, отложите угол a или ускорение(в направлении мгновенного вращения, если n противоположно, в противоположном направлении, n Инжир. 15. Замедление), получим полулинию, где имеется мгновенный центр ускорения Q на расстоянии i4Q(рисунок (>.15)).
Смотрите также:
Предмет теоретическая механика
| Скорости точек плоской фигуры | План скоростей и план ускорения |
| Подвижная и неподвижная центроиды | Сложение вращений твердого тела вокруг параллельных осей |

