Ускорение Кориолиса

Ускорение Кориолиса

• Рассмотрим ускорение Кориолиса и его свойства. Определяется по уравнению (10) 2.-2 («.k»,). Угловая скорость вращающейся части движения подвижной системы отсчета, то есть угловая скорость переносного движения (б. Ускорение Кориолиса является результатом взаимодействия двух фигоподобных и относительных движений. Часть этого (w, hvg) получается путем изменения переносной скорости точки из-за относительного движения. Другая его часть (yechsg) является результатом изменения относительной скорости из-за определенного движения.

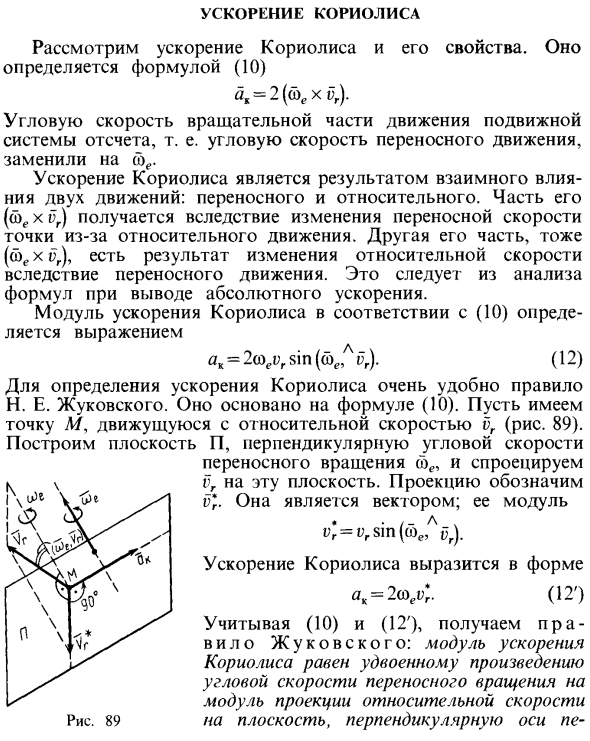
Это получается из анализа формулы при выводе абсолютного ускорения. Коэффициент ускорения Кориолиса согласно (10) представляет собой формулу at = 2weDrsin («e, At; r). (12) Правила Н. Е. Жуковского очень полезны при определении ускорения Кориолиса. Это основано на уравнении (10). Предположим, что существует точка M, которая движется с относительной скоростью vr (рис. 89). Создайте плоскость, перпендикулярную угловой скорости переносимого нами вращения, и спроецируйте vr на эту плоскость. Проекция обозначена v * r. Она вектор. Его модуль v * = «rsin (cbe, π). Ускорение Кориолиса выражается в виде a, = 2a> X. (12 ‘) Учитывая (10) и (12 ‘), мы можем получить правила Жуковского.

Для построения этого уравнения необходимо было иметь в виду, что сумма моментов обеих сил, составляющих ось, в точности равна моменту H для оси. Людмила Фирмаль

Коэффициент ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости. Рис. 89 Плоскость, перпендикулярная оси ne Вращение Вращение: Чтобы получить направление ускорения Кориолиса, спроецированный вектор относительной скорости v * должен быть повернут на 90 ° вокруг оси, параллельной оси переносного вращения в этом направлении вращения. Рассмотрим случай, когда ускорение Кориолиса исчезает. Из (12), «, = 0 в следующих случаях. 1) соя = 0, т.е. мобильное движение поступательное. 2) o, = 0, то есть момент, когда направление относительного движения изменяется. 3) Когда sin (a> e, d,) = 0, то есть относительная скорость движения vr параллельна угловой скорости переносного вращения r> e.

• Обратите внимание, что ускорение Кориолиса отличается, когда одно и то же движение в абсолютных точках разлагается в форме, похожем на фигуру, и относительно другим способом. Пример 1. Радиус 7? = 1 м шар вращается вокруг вертикальной оси O / по закону φ = 2 / ~ рад. Точка M движется вдоль меридиана шара по закону s = rW2 / 4 (рис. 90, а). Расстояние z измеряется от точки на меридиане Мо. Определить абсолютную скорость и ускорение точки М в момент времени / = 1 с. Решения. Для конкретного движения точки возьмите его вращение с шаром вокруг оси Og (рисунок 90.6). В этом случае относительное движение точки будет происходить вдоль меридиана шара. Определить положение точки М на меридиане в момент времени t = 1 с. Существует г = к / 4м. Поскольку R = l m, положение точки определяется широтой a = n / 4.

Рассчитайте угловую скорость переносного движения. получить f = 2 — 3 ”2; при / = 1 с f = -1 с” ’ось w = | f | = 1 с -1 знак минус yφ указывает, что вращение шарика происходит с отрицательной стороны угла = Ru> cosa. = y / 2l2isO, лм / с. Скорость относительного перемещения точки, = | 1 |, где s = iuj2. Следовательно, если / = 1 с $ = i / 2 = 1,6 м / с, то в = 1,6 м / с. Знак плюс для j указывает на то, что in направлено на увеличение s. В рассматриваемом случае Ie направлено вдоль касательной параллельно контейнеру и перпендикулярно v, которое направлено вдоль касательной к меридиану. так Поскольку переносное движение — это вращение шарика вокруг неподвижной оси, абсолютное ускорение точки определяется по формуле (А).

Следовательно, должно быть две линии, которые пересекают все пять линий одновременно, или, говоря языком геометрии линии, данные пять линий принадлежат линейной конгруэнтности. Людмила Фирмаль

Портативное нормальное ускорение a «r = r ;, где и ‘, является проекцией b на плоскость, перпендикулярную переносной оси вращения Oz’. У нас есть «; = I>, sina = l, 6N / 2/2 l, l m / s. Затем найдите a = 2-1 • 1,1 = 2,2 м / с2. Чтобы определить направление a, «; поверните ось Mz параллельно Oz в направлении вращения переносного устройства, то есть« 90 »по часовой стрелке, если рассматривается. Вы можете видеть, что ускорение a ориентировано вдоль ускорения a’g. Чтобы определить абсолютное ускорение, рассмотрите направление ускорения компонента, выберите декартову координатную ось Mxyz и спроецируйте обе части векторного уравнения (a) на эти оси (рисунок 90.6). а = а; + в этих двух направлениях дает: o, = «sin «, = 16,8 см / с2.

Направление ускорения a — это вектор v ‘вокруг оси, проходящей через точку M, параллельной вращению стержня Og в направлении дуги, стрелка w Получается вращением r на 90 градусов. Выберите оси координат Mx’y и спроецируйте вектор, входящий в уравнение (a), на эти оси. У нас есть: Из этих уравнений определяется неизвестное ускорение. а = греха <р + а! «-51,8 см / с2; а, = a cos q> — а, = 30,5 см / с2. Ускорение а оказалось отрицательным. В результате предположение о направлении оказалось неверным. На самом деле, а указывает в ранее принятом направлении. Ускорение а оказалось положительным. Предположение о направлении дуги c было подтверждено. Угловое ускорение стержня определяется по формуле b = | b; | / OL / = 6,1 с’2.

Смотрите также:

Задачи по теоретической механике

Сложение скоростей	Сложение движений твердого тела
Сложение ускорений точки в общем случае переносного движения	Сложение поступательных движений твердого тела

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.