Оглавление:




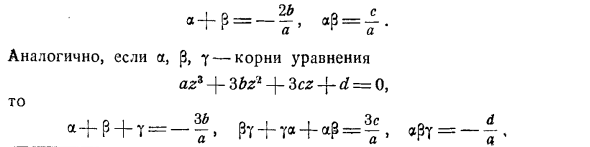
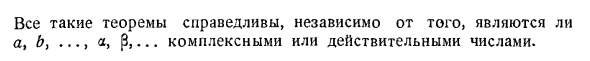
Уравнения z*-{-l =0
- Уравнение z * — {- l = Oy az * + 2bz -f- c = 0. z? Существует действительное число z, подобное -F-l = 0; Мы говорим, что это уравнение не имеет реальных корней. Однако, как мы уже видели, комплексные числа / и -i удовлетворяют этому уравнению. Мы говорим, что это уравнение имеет два сложных корня i и –i. Поскольку я удовлетворяю уравнению z * = -1, оно может быть записано в виде -1. Комплексные числа иногда называют мнимыми числами. Но «воображаемые числа» не являются «воображаемыми числами» в обычном значении слова, чем «действительные» числа или другие математические понятия.
Как поймет читатель из предыдущих соображений, комплексное число представляет собой пару чисел (x: y), объединенных в символ, чтобы ими можно было манипулировать в форме x — \ — yi. так / = 0 + 1 / Он записывается вместо пары чисел (0, 1) и может быть геометрически представлен точкой или смещением [0, 1]. И когда я говорю, что это корень уравнения z * — {- 1 = 0, это означает, что мы определили способ объединения таких пар чисел (или смесей). (0,1) сама дает пару (-1,0). Теперь рассмотрим более общее уравнение az4 -f- 2bz -f- c = 0, Где ay c — действительное число. Если АСУ, обычное решение дает вам две настоящие Кореи
Вещественные числа не совпадают с рациональными числами, а комплексные числа не совпадают с действительными числами. Людмила Фирмаль
Для b * ac уравнение не имеет реальных корней. Может быть написано как / ac-no (* + «) = — Один или Плекс номер-b2) \ уравнение Есть два сложных маршрута B ^ iV ac-br — «* * * а-а Для b * = -ac ^, если уравнение заполнено только одним значением x, то есть, если вы согласны с тем, что уравнение — ^ имеет два одинаковых корня, квадратное уравнение с вещественным коэффициентом Во всех случаях есть два корня: два разных реальных маршрута, или два идентичных реальных маршрута, или два разных составных маршрута.
Поскольку допускаются сложные корни, естественно возникает вопрос о том, может ли квадратное уравнение иметь более одного корня. Легко понять, что это невозможно. Доказательство может быть выполнено с использованием тех же аргументов, которые используются в первичной алгебре для доказательства того, что уравнение порядка n не может иметь более n действительных корней. Комплексное число x — {- yi представлено одной буквой z. То есть напишите z = x — \ — yi. f (z) означает r многочлен с действительными или комплексными коэффициентами. Тогда последовательно докажи (1) Остаток, когда f (z) делится на z-a (a является действительным или комплексным числом), равен / (a). (2) Если a является корнем уравнения f (z) = i 0, f (z) делится на z-a без остатка; (3) Если f (z) является полиномом n-го порядка и f (z) -0 имеет n корней a, a2, a,
| Комплексные числа | Диаграмма Аргана |
| Геометрическое толкование умножения на i | Корни из комплексных чисел |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- f (z) = A (z-ax) {z-a%) … (z-an), Где A — действительная или комплексная постоянная, то есть коэффициент zn of / (z). Из этого окончательного результата и теоремы § 40, f (z) не может иметь более n корней. Квадратичное уравнение с действительными коэффициентами имеет два корня. Также видно, что та же теорема справедлива для уравнений любого порядка. Действительный или комплексный коэффициент: уравнение порядка n имеет ровно n корней. Единственная трудная часть доказательства состоит в том, что уравнение должно иметь хотя бы один корень. Мне нужно отложить доказательство этого пункта ».
Реальная теория начинается с понятий положительных целых чисел, сложения и умножения и противоположного действия (вычитание и деление). Вы можете видеть, что эти действия не всегда осуществимы, если не введен новый тип номера. Если вы введете отрицательное число или коэффициент, вы можете назначить конкретное значение разницы 3-7 Y, чтобы ввести рациональное число. Если развернуть всю арифметическую операцию, включая извлечение корня и решение уравнений, вы увидите, что это невозможно без расширения некоторых из этих действий (например, извлечения квадратного корня из числа, которое не является точным квадратом).
Однако сразу можно заметить одно очень интересное следствие этой теоремы. Людмила Фирмаль
Числовое понятие и гл. I. Как сделано в этой главе, никакие дальнейшие действия невозможны, такие как извлечение квадратного корня из -1, без дальнейшего продвижения и введения комплексных чисел. Учитывая уравнения более высокого порядка, естественно предположить, что некоторые из них могут стать неразрешимыми даже по отношению к комплексным числам и, следовательно, столкнуться с необходимостью введения других типов чисел. Тот факт, что корень алгебраического уравнения является нормальным комплексным числом, указывает, что это не так.
Все основные теоремы алгебры, доказанные применением только правил сложения и умножения, остаются в силе независимо от того, являются ли числа, появляющиеся в них, действительными или сложными. Эти правила применяются не только к действительным числам, но и к комплексным числам. Например, если вы знаете, что а и р являются корнями уравнения тогда 1 р а г а Точно так же, (3,? az3 + 3 & g? + + d = 0, тогда + T = + + ^ = «RTВсе такие теоремы верны независимо от того, являются ли a, b, a, p, … комплексными или действительными.

