Уравнения вида f(x)=g(x) где f(x)≤A, a g(x)≥A и другие задачи этого типа. Метод оценок

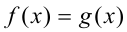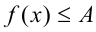Уравнения вида где , a 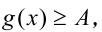, и другие задачи этого типа. Метод оценок

Уравнения вида

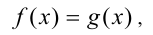
где функции, расположенные в левой и правой частях, удовлетворяют оценкам 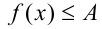, a 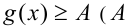— фиксированное число), равносильны на ОДЗ системе

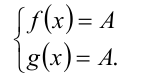
Здесь существенно используется ограниченность на ОДЗ функци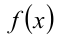й и 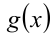. Так как при использовании этого метода приходится независимо друг от друга оценивать возможные значения левой и правой частей уравнения, то метод иногда называют методом оценок.

Существуют и другие разновидности этого метода, например, если при решении уравнения

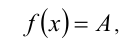
где 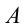— некоторая заданная константа, оказывается, что наибольшее (наименьшее) значение функции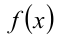, стоящей в левой части данного уравнения и рассмотренной на ОДЗ уравнения, совпадает с 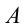, то решениями уравнения будут как раз те значения неизвестной 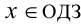, при которых 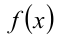достигает своего наибольшего (наименьшего) значения, и надо лишь отследить все те значения 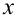, при которых неравенство 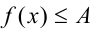(соответственно 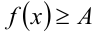) обращается в равенство.

В другой ситуации требуется решить неравенство вида

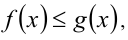
и при анализе и независимом оценивании значений функций 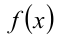, 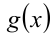на ОДЗ задачи оказалось, что эти функции удовлетворяют оценкам в виде неравенств:

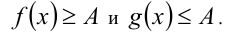
Тогда имеем тройное неравенство 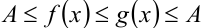, необходимым и достаточным условиием выполнения которого является одновременное обращение всех трёх неравенств в равенства. Таким образом, исходное неравенство сводится к равносильной ему на ОДЗ системе уравнений

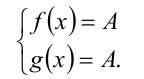
Пример №372.

Решить уравнение

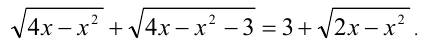
Решение:

Воспользуемся для решения задачи методом оценок. Вначале выделим полные квадраты под знаками радикалов в левой части уравнения:

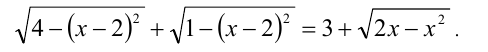
Теперь хорошо видно, что 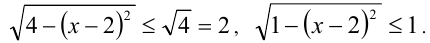Из этих оценок следует, что левая часть уравнения принимает на ОДЗ значения, меньшие либо равные 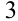, в то время как правая часть уравнения больше либо равна 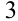. Это означает, что решаемое уравнение равносильно системе уравнений

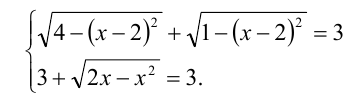
Ответ: .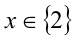

Пример №373.

Решить уравнение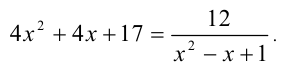

Решение:

Перепишем это уравнение в виде
320

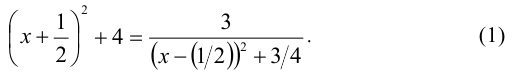
Очевидно, что для любых действительных 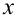имеем оценки:

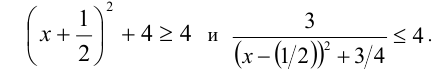
Следовательно, уравнение (1) равносильно системе уравнений

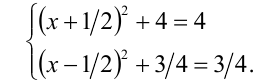
Эта система уравнений не имеет решений, поэтому исходное уравнение также не имеет решений.

Пример №374.

Решить уравнение

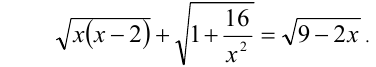
Решение:

ОДЗ: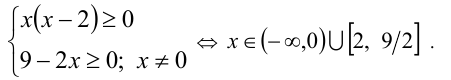

Возведём на ОДЗ обе части уравнения в квадрат и после упрощения получим:

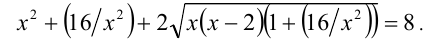
Применяя неравенство 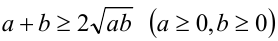, полагая в нём 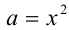, 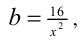получим, что 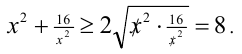Поскольку, кроме того 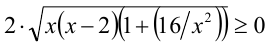, то левая часть неравенства принимает на ОДЗ значения большие либо равные 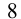, а правая часть уравнения при этом равна 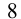. Отсюда следует, что уравнение выполняется тогда и только тогда, когда левая часть достигает своего наименьшего значения, равного 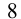, т.е. уравнение равно сильно системе двух уравнений 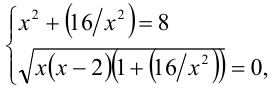решая которую, находим решение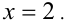

Пример №375.

Решить неравенство

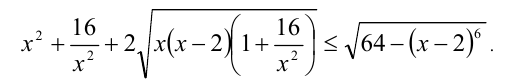
Решение:

Решая предыдущую задачу, мы показали, что левая часть в данном неравенстве принимает на ОДЗ значения большие либо разные 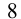. Заметим, что правая часть неравенства принимает на ОДЗ значения меньшие либо равные 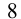. Таким образом, данное неравенство может выполняться тогда и только тогда, когда справедлива система условий

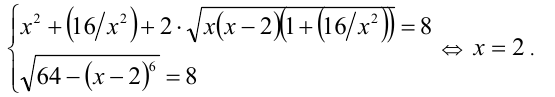
К группе задач, решаемых методом оценок, можно отнести решение уравнений вида

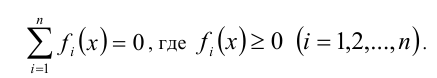
Такое уравнение сводится к решению равносильной ему системы

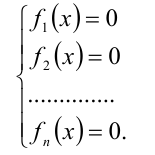
Пример №376.

Найти действительные корни уравнения

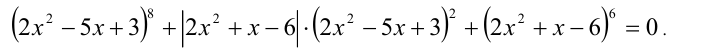
Решение:

Данное уравнение как раз относится к указанному типу. Сумма трёх неотрицательных слагаемых может обращаться в нуль тогда и только тогда, когда все они одновременно обращаются в нуль, т.е. уравнение равносильно системе уравнений

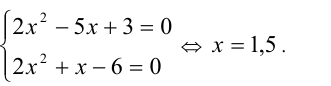
Рассмотрим ещё несколько примеров, когда использование различных алгебраических неравенств позволяет получать необходимые оценки, с помощью которых затем находится решение.

Пример №377.

Решить уравнение

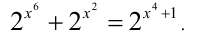
Решение:

Воспользуемся неравенством между средним арифметическим и средним геометрическим 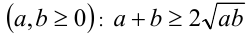(неравенство обращается в равенство 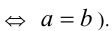Положим в нём 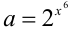, 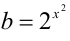. Получаем первую оценку:

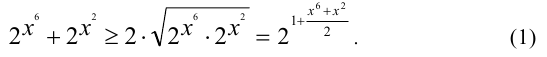
Далее, ещё раз воспользуемся неравенством, положив на этот раз 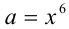, 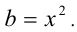Тогда получим вторую оценку

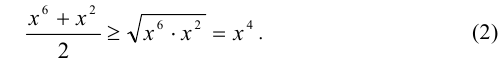
Подставляя (2) в (1), получим неравенство

Из неравенств (1) и (3) по свойству транзитивности заключаем, что

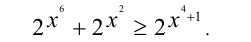
Чтобы это неравенство обращалось в равенство, необходимо и достаточно, чтобы оба неравенства (1) и (2) одновременно обращались в равенства, т.е. чтобы

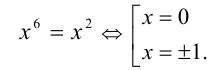
Ответ: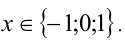

Пример №378.

Решить уравнение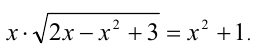

Решение:

Так как 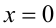, очевидно, не является корнем уравнения (более того, так как правая часть больше нуля, то и левая часть больше нуля, а значит 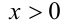), то поделим на 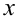обе части уравнения:

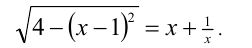
Левая часть уравнения меньше либо равна 2, а правая — больше либо равна 2 (здесь мы применили известное алгебраическое неравенство о сумме двух положительных взаимно обратных чисел), следовательно, равенство возможно тогда и только тогда, когда

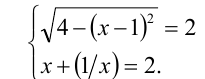
Ответ: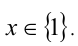

Пример №379.

Решить систему

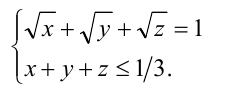
Решение:

Воспользуемся для решения задачи вспомогательным алгебраическим неравенством

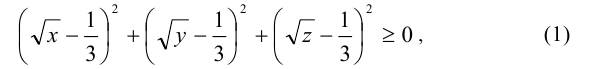
или

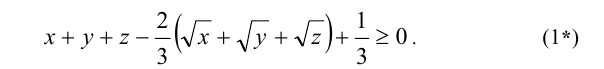
Поскольку в силу первого уравнения системы 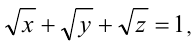то из 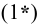получаем оценку 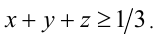С другой стороны, в силу 2-го неравенства системы 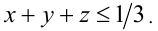Следовательно, 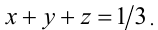Но это возможно тогда и только тогда, когда неравенство (1) обращается в равенство, т.е. 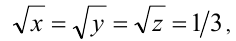а значит,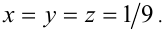

Ответ: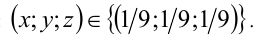

Пример №380.

Решить уравнение

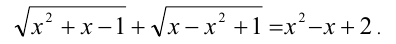
Решение:

Воспользуемся неравенством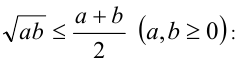

На ОДЗ имеем: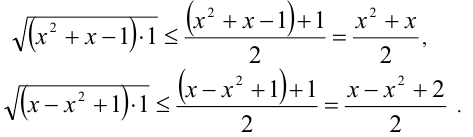

Складывая почленно эти неравенства, получим неравенство-следствие

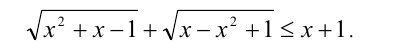
Заменим в силу исходного уравнения сумму радикалов на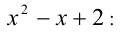

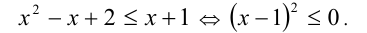
Проверкой убеждаемся, что 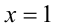удовлетворяет исходному уравнению.

Пример №381.

Решить уравнение

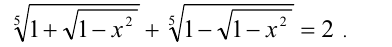
Решение:

Согласно неравенству Бернулл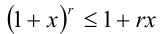и , при 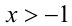, 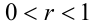имеем

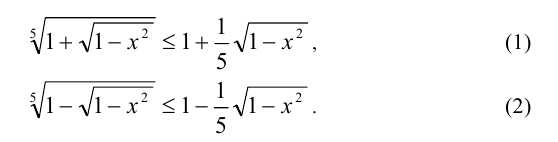
Складывая неравенства почленно, получим оценку

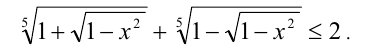
Заметим, что последнее неравенство обращается в равенство тогда и только тогда, когда неравенства (1) и (2) одновременно обращаются в равенство, т.е. при условии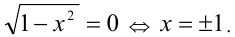

Ответ: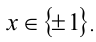

Пример №382.

Решить уравнение

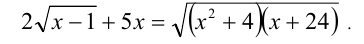
Решение:

ОДЗ: 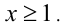1-й способ. Воспользуемся неравенством Коши-Буняковского: для любых действительных 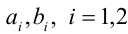, имеем

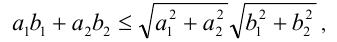
причём неравенство обращается в равенство тогда и только тогда, когда или все числа 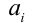одновременно равны нулю (или все 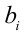одновременно равны нулю), или существует такое 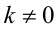, что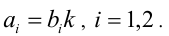

Положим 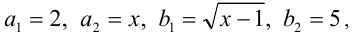тогда неравенство Коши-Буняковского примет вид

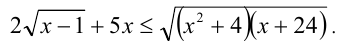
По условию неравенство обращается в равенство. В данной задаче это возможно, только если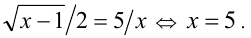

2-й способ. Рассмотрим два ненулевых вектора 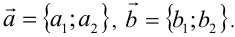По определению скалярного произведения имеем

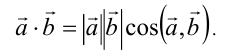
Используя оценку 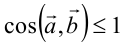, получим векторный аналог неравенства Коши-Буняковского: 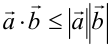или, переходя к координатам векторов,

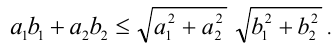
Заметим, что данное неравенство обращается в равенство тогда и только тогда, когда векторы 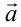и 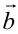сонаправлены, т.е. когда их соответствующие координаты одновременно равны нулю или имеют один знак и пропорциональны.

Положим 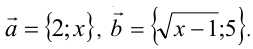По условию неравенство обращается в равенство, а это возможно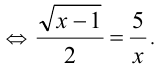

3-й способ. Уравнение можно было решить возведением на ОДЗ в квадрат, при этом получается уравнение

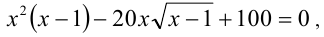
которое заменой 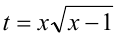сводится к квадратному. Ответ: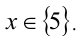

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Предмет математика

Эти страницы возможно вам будут полезны:

Графический подход (метод координат) при решении уравнений и неравенств с примерами решения

Умножение на функцию при решении уравнений и неравенств с примерами решения

Уравнения и неравенства вида f(x)=g(x), f(x)<g(x), где функции f(x) и g (x) имеют разную монотонность

Уравнения и неравенства вида φ (f(x))=φ(g(x))<φ(g(x)), где φ(x) строго монотонная функция