


- Далее мы обсудим вывод уравнения движения реальной жидкости. Эти уравнения, основанные на втором законе Ньютона, позволяют определить характер изменения скорости пространства. С их помощью можно также определить объем, например, перепад давления при движении ламинарного потока. Эти уравнения, хотя и слегка модифицированные, применимы к турбулентному движению, и рассматриваются их приложения separately. In в следующем представлении предполагается, что поток является ламинарным потоком.
Второй способ применения Ньютона к жидким элементам Напишите уравнение движения в направлении 3-х осей. Для оси X РХ =Макс(11.1) Это уравнение может быть описано скоростью изменения импульса. DH. (11.2) Примените это уравнение к жидким элементам, которые имеют постоянную массу и движутся вместе с жидкостью. Это метод Лагранжа, согласно Chapp. 10 соображения, уравнение (11. 2) Перейти к дифференциальной записи в виде существенного дифференциала: (11.3) Для простой величины p c1x d, y Ar уравнение (I. 3) имеет вид = Р переменного тока. (11.4) массовая сила Сила aHx-это результирующая сила, действующая на элемент по оси x direction.
Удобно подразделить их на массовые Силы Х, которые измеряются при Н / кг = м / с2, и те, которые обусловлены механическими напряжениями, действующими на поверхности элементов. Массовая сила действует на весь объем element. An примером этого является сила, действующая на объект, заряженный электрическим полем. Массовая составляющая силы в направлении оси X равпа для выбранного элемента добро пожаловать. (11.5) Единственной рассматриваемой массовой силой является гравитация. Некомпоненты могут быть представлены следующим образом Х =?Co8p (I. Six) Где P-угол между осью X и направлением силы тяжести.
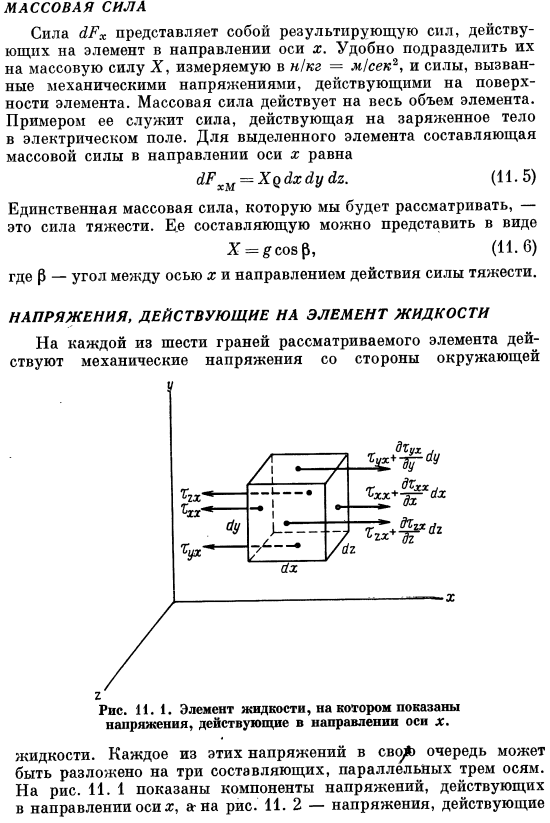
- Напряжение, действующее на жидкий элемент В каждой из 6 плоскостей рассматриваемых элементов механическое напряжение от периметра напряжение, действующее вдоль оси X. Жидкость. Каждое из этих напряжений может быть разложено на 3 компонента параллельно трем осям. На рис. 11.1 показаны компоненты напряжений, действующие в направлении оси i. 11. 2-напряжение, действующее на DAP face. In на этих рисунках индексная система показана в\ \ 1 /т. первый индекс показывает плоскость, на которую действует напряжение, а ось, перпендикулярная этой плоскости, показана. 2-й индекс указывает направление, в котором работает напряжение. Напряжение индекса смешивания (txu) — это напряжение сдвига.
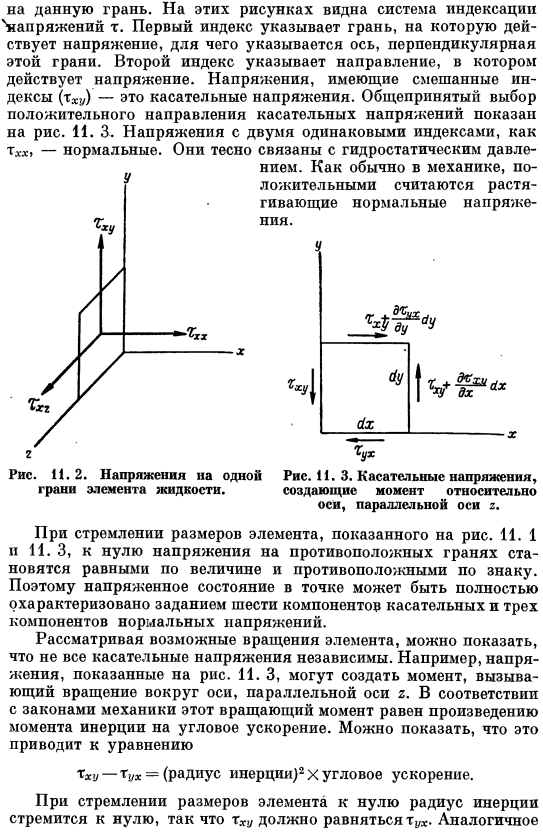
Общепринятый положительный выбор напряжения сдвига показан на рисунке. I. 3. Как и Txx, напряжение с 2 одинаковыми индексами является нормальным. Они тесно связаны с гидростатическими pressure. As обычно в механике нормальное напряжение растяжения считается положительным Ния. Рисунок 11.2.Напряжение на одной стороне текучего элемента. Рис. 11.3.Касательное напряжение, создающее момент на оси, параллельной оси 2. Если размеры элементов показаны на Рисунке 11. 1 и I.
Когда 3 равно нулю, напряжение на противоположной стороне равно по величине и знак равен opposite. So, можно полностью охарактеризовать напряженное состояние точки, указав 6 компонент касательной и 3 компоненты нормального напряжения. Рассматривая возможное вращение элементов, можно видеть, что не все касательные напряжения независимы. Например, напряжение, указанное на схеме. I. 3.
Можно создавать моменты, вызывающие вращение вокруг оси, параллельной оси 2.Согласно законам механики, этот крутящий момент равен произведению момента инерции и углового ускорения. Мы можем показать, что это приводит к уравнениям. thu-Tuh =(радиус инерции) 2 x угловое ускорение. Чт должен быть равен тух, потому что размер элемента стремится к нулю, поэтому радиус инерции стремится к нулю. Аналогичный аргумент указывает на то, что это Ma=ta2x и tauy2=tau2y. обычно давление связано со следующим соотношением к нормальному напряжению: — П = » 3-(txx все + Туу + тг).(11.Семь) Положительное давление соответствует сжатию, а напряжение имеет отрицательный знак, так как напряжение положительное.
