Оглавление:





Уравнения состояния реальных газов
- Все реальные газы являются парами определенной жидкости, и чем ближе газ находится к переходу в жидкое состояние, тем больше отклонение от характеристик идеального газа, а идеальное газовое состояние описывается уравнением Кура-Пейрона. Для качественной оценки свойств экзистенциального газа рассмотрим области со значительными отклонениями от уравнения, объясняющие идеальное поведение Если сжать газ при постоянной температуре, то можно добиться насыщения (сжижения газа), которое соответствует этой температуре и определенному давлению. При дальнейшем сжатии, пар конденсируется и в определенный момент полностью превращается в жидкость.
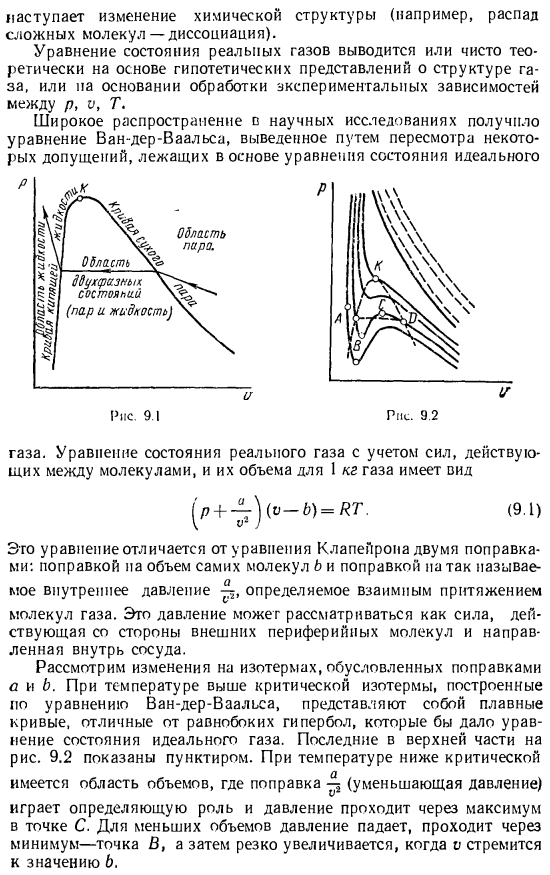
Давление насыщенного пара однозначно определяется его температурой, поэтому процесс перехода пара в жидкость происходит при определенной температуре и давлении. р — » на рис. 9.1 область 2-фазового состояния (пар и жидкость) лежит между кривой кипящей жидкости и сухой насыщенной vapor. As давление возрастает, эти кривые сближаются. Разрыв происходит из-за уменьшения объема пара и увеличения объема liquid. At при определенном давлении, определяемом для конкретной жидкости (пара), кривая кипения жидкости и пара совпадает в так называемой критической точке, которая совпадает с критическим параметром.
Настоящая глава посвящена почти исключительно процессам теплообмена при стационарном режиме. Людмила Фирмаль
Давление crc, температура tcr, удельный объем cr, характеризующие критическое состояние matter. In критическое состояние, разница между жидкостью и паром disappears. It это физическое состояние, которое ограничивает как однородное вещество, так и вещество, которое распалось на 2 phases. At температура выше критической, газ не может конденсироваться при любом давлении. То есть она становится жидкой. В этом случае все газы в области, близкой к сжиженному состоянию, практически воспроизводят соотношение между параметрами состояния по уравнению Клапейрона.
Для всех газов с более или менее значительной плотностью сцеплением между молекулами, объемом, занимаемым ими, и связыванием с группой молекул тоже нельзя пренебрегать. Связывание означает механическое соединение 2 или более молекул с 1 комплексом. Уменьшение числа независимых частиц, составляющих газ, должно привести к увеличению средней молекулярной массы газа и снижению его давления. Эта ассоциация существенно усложняет математическое описание состояния реального газа.
Если понизить давление и увеличить температуру газа, то можно использовать уравнение состояния идеального газа, за исключением газов, находящихся под воздействием высокой температуры. Происходят изменения в химической структуре (например, распад сложных молекул-диссоциация). Уравнение состояния экзистенциального газа выводится чисто теоретически на основе гипотез о структуре газа или на основе обработки экспериментальных зависимостей между p, V, T. Уравнение ван-дер-Ваальса, полученное путем модификации нескольких предположений, лежащих в основе идеального уравнения состояния, широко используется в научных исследованиях.
Эта формула отличается от формулы Клапейрона двумя способами: коррекцией объема самой молекулы L и коррекцией так называемого внутреннего давления, которое определяется взаимным притяжением молекул газа. Это давление действует на стороны внешней периферической молекулы и может рассматриваться как сила, направленная к кровеносному сосуду. Рассмотрим изменение Изотерм с поправкой а и B. At температура выше критической изотермы, построенной по уравнению ван-дер-Ваальса, становится гладкой кривой, отличной от биссектрисной гиперболы, дающей уравнение состояния идеального газа. Последний пункт 9.2 в верхней части рисунка обозначен пунктиром.
Температуры ниже критической температуры, поправка играет решающую роль, есть область объема, в которой давление проходит через максимальное значение в точке C. In в случае малого объема давление уменьшается, проходя через минимальное значение-точку B, и по мере приближения к этому значению оно резко возрастает.
При критической температуре максимальные и минимальные значения Изотерм объединяются в точке перегиба K, а касательные Изотерм в критической точке являются горизонтальными, поэтому они должны соответствовать условиям критической точки Получить уравнение отсюда (9.2) (9.3) (9.4) Температура Tvr и объем o r могут быть определены из уравнений (9.3) и (9.4), а давление rvr может быть определено из уравнения (9.1). в результате、 Тр = _〜_. о= 36. «Р etda, СГ’ — «о, 27б’ (9.5) Из последнего соотношения можно определить индивидуальные константы a и f, зависящие от физических характеристик конкретного газа.
- Этот процесс выполняется последовательно, так как переход из жидкого состояния в газообразное протекает при постоянном T и p. It поддерживает 40. Однако сечения AB и CO на изотерме могут быть воспроизведены экспериментально только при использовании очень чистых жидкостей и газов. Вещества в этих областях имеют вид перегретой жидкости и пересыщенного (переохлажденного) пара. Такое состояние называется метастабильным, если вещество остается в водной фазе и не разлагается на фазу.
Основное значение уравнения ван-дер-Ваальса состоит в том, чтобы качественно и точно описать непрерывность перехода из жидкого состояния в газообразное, а дальнейшее развитие уравнения состояния привело к уточнению расчетов и совершенствованию теории. Коэффициент Li6 предполагался нестабильным, но в связи с тем, что он зависит от температуры и объема, были предприняты попытки его улучшить. Однако эти попытки не привели к созданию уравнения состояния, описывающего свойства газов в широком диапазоне параметров.
Разработаны также некоторые характерные соотношения, которые будут обсуждаться в следующей главе. Людмила Фирмаль
Неспособность создать общее уравнение состояния привела к появлению многих эмпирических уравнений, которые могли бы предсказать поведение реального газа с достаточной точностью при различных условиях. Наиболее известными из них являются: 5 эмпирически определенных уравнений Битти-бридмана Константа и уравнение Бенедикта-Уэбба-Рубина, содержащее 8 эмпирических констант — (a, b, d, Ao, Bn, Co и др.).
Вид уравнения Битти-Бриджмена, которое применяется к давлению порядка 250 бар и плотности газа, не превышающей 0,5 в критической точке Рог= это Уравнение состояния Бенедикта-Уэбба-Рубина Эти уравнения позволяют прогнозировать свойства p, V и T-газов с погрешностью в несколько десятков процентов, и, несмотря на их сложность, развитие вычислительной техники облегчит использование таких уравнений состояния в обычных технических расчетах 1. уравнение Вукаловича-Новикова, являющееся одним из самых современных уравнений газовых состояний, учитывает связывание молекул и хорошо согласуется с экспериментальными данными.
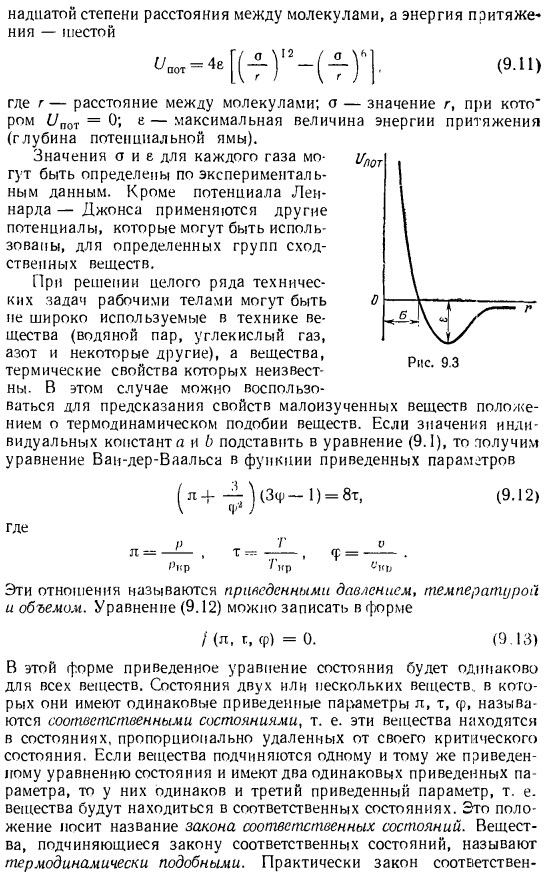
Принимая во внимание столкновение бинарных молекул, это уравнение принимает вид Здесь сито является экспериментальной константой. В настоящее время уравнение состояния теоретически обосновано. Это разложение степени сжатия r в бесконечный ряд степеней 1 / O. (9.10)) Где B, C и O-2-й, 3-й и 4-й вириальные коэффициенты соответственно, учитывающие взаимодействие таких молекул, как 2, 3 и 4.Коэффициент вириала зависит Если зависимость известна, то она определяется только при температуре 1 Тл Потенциальная энергия и молекулярные взаимодействия 1 / oot Встаньте между ними (рис.
Вместо точной аналитической зависимости (7PST = /®) фактически используется приближенная формула, называемая потенциалом. Широко используется потенциал Леонарда Джонса, энергия отскока пропорциональна 2 Степень расстояния между молекулами и энергия притяжения равна 6-й (9.Я) g r g-расстояние между молекулами. a-величина r, где Upot = 0, e-максимум энергии притяжения (глубина потенциальной ямы). Значения A и b для каждого газа можно определить по экспериментальным данным. Помимо потенциала Леппарда-Джонса, используются и другие потенциалы, которые могут быть использованы для конкретной группы аналогов.
При решении некоторых технических задач рабочим телом является вещество, которое не находит широкого применения в технике (водяной пар, углекислый газ, азот и др.), но имеет неизвестный тепловой properties. In в этом случае, благодаря термодинамическому сходству веществ, они могут быть использованы для прогнозирования свойств веществ, которые слабо изучены. Если визуальная константа постоянна и b подставляется в уравнение (9.1): функция уравнения Вая-дер-Вааля приведенного параметра Эти отношения называются уменьшением давления, температуры и объема. Выражение (9.12) может быть записано в следующем виде: /(Л, Р ₽)= 0.
В таком виде данное уравнение состояния будет одинаковым для всех веществ. Состояние 2 или более веществ с одинаковыми параметрами восстановления n, m, p называется соответствующим состоянием. То есть эти вещества находятся в состоянии, пропорционально отделенном от критического состояния. Если вещество следует одному и тому же уравнению состояния восстановления и имеет 2 идентичных параметра восстановления, то они имеют один и тот же 3-й параметр восстановления. То есть субстанция становится соответствующим состоянием. Это положение называется законом каждого государства. Вещества, подчиняющиеся законам соответствующего состояния, называются термодинамически similar.
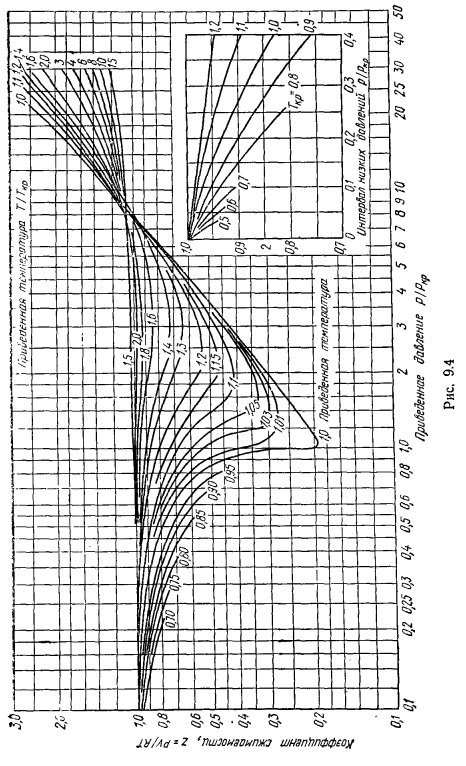
Факт, закон Удобнее всего использовать эти состояния в виде зависимости r = 1 (n, r), а для расчета можно использовать (R-^ -диаграмма (рис.9.4)).Зная важные параметры вещества, найдены l = — D-и m =, коэффициент сжатия этих параметров определяется из диаграммы R-l, соотношение которых вычисляется по формуле. Закон соответствующего состояния практически только соблюдается, поэтому точность расчетов по этому методу не превышает 15%.Поэтому для идентичных литов коэффициент сжатия должен быть равен, а коэффициент сжатия в критической точке rcr = — * 1*должен быть равен.
Смотрите также:
| Дифференциальные соотношения для теплоемкостей | Водяной пар. Парообразование при постоянном давлении |
| Термические коэффициенты | Изменение агрегатного состояния |

