Оглавление:





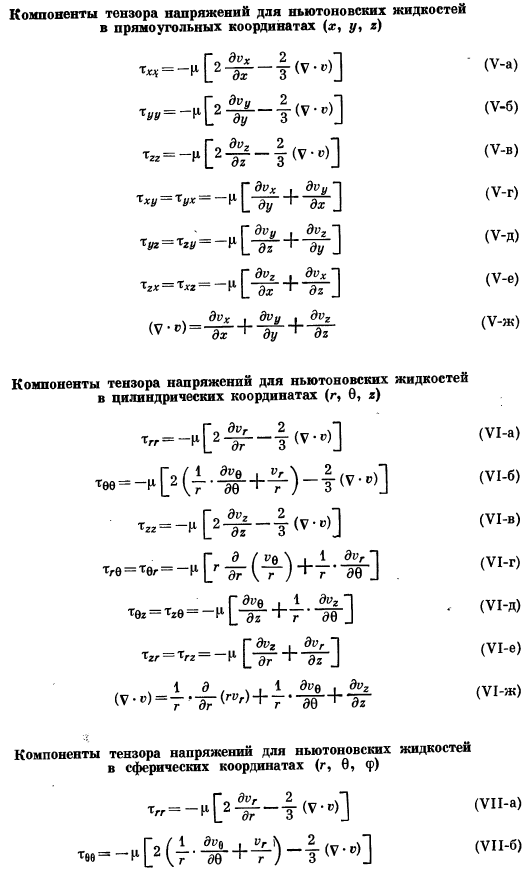


Уравнения сохранения в криволинейных координатах
- Вы можете видеть, что все выводы в предыдущем разделе этой главы сделаны в декартовых координатах для простоты. Однако, при решении задачи, декартовы координаты не всегда являются наиболее распространенными. Глава 2 уже указывает, что криволинейные координаты могут быть более полезными. Например, в случае потока Häagen-Dazs, в случае Häagen-Dazs. Скорость оси является функцией только 1 переменной величины. R — это 2r. Точно так же усложняется математическая церемония имен труб. При анализе обтекания сферы использование сферических координат позволило описать поле скоростей только 2 координатами y, а»e» — «x, r>», r>r, что привело к упрощению граничных условий.
Он может быть вычислен, если известен коэффициент теплообмена, который определяется уравнением где п обозначает направление, перпендикулярное к поверхности стенки. Людмила Фирмаль
Аналогичная проблема возникает и при применении группы прямых линий к формуле защиты с одной культурой. Уравнения непрерывности и движения формальных уравнений, полученных в разделах 3.1 и 3.2, выражаются в виде Y, Y, R, компонента b X, yrh и компоненты напряжений. Если вы хотите описать эти уравнения непосредственно в терминах, вам нужно написать следующее: А)отношение между x, y, r и r, 0,p. б) отношение между r>x, yy, yy и соответствующей компонентой, e>Irθ в) mn, M x N, M x n, YY, YY) из которых. Переход от прямоугольного выбора может быть осуществлен путем выполнения процедуры, в которой прямая одиночная связь является длинной.
- Ниже и везде в книге, прямоугольные, цилиндрические и сферические координаты * являются записью основных уравнений. Поэтому читатель не обязан выполнять указанные операции. Здесь можно легко получить непрерывное уравнение в криволинейных координатах, составляющих массовый баланс тонкого слоя, но предупреждаю читателя, что этого нельзя делать при выводе уравнения motion.
Таким образом, можно утверждать, что поля скорости и давления для установившегося потока жидкости с постоянными свойствами подобны, когда существует геометрическое подобие границ полей, когда скорости вдоль границ подобны и когда критерий Рейнольдса имеет постоянную величину. Людмила Фирмаль
В целом, этот метод не рекомендуется для таких случаев, так как метод балансировки тонкого слоя можно сказать, что его довольно трудно применить к системам, где линия потока является curved. As определенный в разделе 3.5, он является самым простым для построения из одного уравнения. Х, Y, х): + +(1″| )±^-(р|’г’ =О’ △(Г, 0,г): +tперед)+↓ ⁽ Координаты поверхности (r, 0,₽): (1-а) (1-6) *Видеть. — .Эд. △(Г, 0,Л) См. № 2 0 компонентов 0. расщеплять.
Смотрите также:
| Уравнение движения | Применение уравнений сохранения для решения задач об установившихся течениях |
| Уравнение механической энергии | Уравнения сохранения для несжимаемых неньютоновских жидкостей |

