Оглавление:




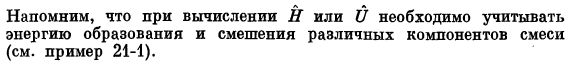

Уравнения сохранения для многокомпонентных смесей, выраженные через потоки
- Главы 3 и 10 вывели уравнение сохранения чистой жидкости. Далее мы расширяем эти выражения, чтобы получить уравнение сохранения для неизотермических многокомпонентных жидкостей, состоящих из n химически различных веществ. 1.Уравнения неразрывности для каждого вещества, присутствующего в жидкости: — ^- Р О= -Р *(х»)- (В-Д + П» = 1. Если вы добавите все n подобных уравнений, вы получите уравнение неразрывности (17.8) смеси. Любое из приведенных выше N уравнений может заменить задачу в уравнении неразрывности смеси. 2.Уравнение движения смеси: (17.21) (17.22). Здесь, чтобы сократить обозначение, мы ввели Тензор давления i = m + + pb.
Где m-компонент импульсного потока, обусловленный вязкостью (или тензором напряжения сдвига). Р-статическое давление. b-единичный Тензор. Заметим, что уравнение (17.22) не тождественно уравнению движения чистой жидкости[опорное уравнение (3.9) pg заменено на 2 PrfTr только последним членом 1.При составлении этого термина различная внешняя сила g «действовать» может влиять на химический состав смеси для каждой единицы массы G.
Охлаждающая пленка постепенно разрушается путем смешения с горячими газами, так что ее эффективность уменьшается по направлению потока. Людмила Фирмаль
Уравнение энергии смеси: (17.23) Заметим, что это уравнение отличается по форме от уравнения энергии чистой жидкости, где произведение (pv-g) заменяется на S; (N-g’) только в последнем члене эталонного уравнения (10.11).Здесь d-поток энергии многокомпонентной смеси для средней массовой скорости v, определение которой приведено в разделе 17.4.Выброс и поглощение энергии излучением игнорируется. Уравнение(17.21) — (17.23) позволяет получить полное описание процессов и величину энергии массопереноса в многокомпонентной системе. system. In кроме того, необходима информация об уравнении состояния P P (P, T, ₍x), термическом уравнении U = U (p, T, x.) состояния и скорости химической реакции.
Наконец, в общем случае, все, что вам нужно, это Полностью полная зависимость потока y;, l и q. It представлен наклоном соответствующей переменной и коэффициентом передачи (см. раздел 17.4).Зависимость коэффициента переноса от p, T и состава также должна быть известна. Ранее при обсуждении уравнения сохранения уже указывалось, что оно может принимать множество различных форм в зависимости от следующих условий: а)используется ли D / Dt или d / dt -; б)какая система координат используется для описания потока в)используются ли единицы массы или единицы моля. г) Способ высвобождения различных форм энергии.
- Например, можно переписать уравнение (17.21)-(17.23) следующим образом: Непрерывные уравнения п; =〜(В•{П /+ Л))+ Уравнение движения Уравнение энергии Согласно таблице. 15.3, величина выражения (17.24) (r. o + A) равна массовому потоку ng для фиксированной системы координат. Аналогичные потоки могут быть введены в случае передачи импульса и энергии. Таким образом, поток массы, импульса и энергии в систему координат, зафиксированную в пространстве, определяется соотношением.
Уравнение энергии dt (17.32) Уравнение(17.24)-(17.26) можно переписать: уравнение неразрывности Уравнение движения Потоки π и Φ остаются постоянными, и r очень полезен при формулировке утверждений. В случае одномерных стационарных задач при отсутствии химических реакций или внешних сил потоки nφφ и e остаются constant. In в частности, потоки N и e очень удобны для постановки задачи совместного переноса тепла и вещества(пример 17-1 В заключение сделаем несколько замечаний относительно особой формы уравнения движения и энергии. В разделе 10.3 мы отметили, что уравнение движения в форме, обычно записываемой, полезно для обобщения проблемы вынужденной конвекции.
Верхнее правое устройство показывает процесс пленочного охлаждения, при котором струя охладителя продувается через ряд разрезов в направлении, касательном к поверхности. Людмила Фирмаль
Однако другие формы опорного уравнения (10.29) 1 более пригодны для характеристики ограниченных случаев чистой естественной конвекции, возникающих в результате неравенства температур в системе. Для систем с неоднородным распределением концентрации и для систем с неоднородным распределением температуры опишите уравнение движения в виде (10.28) и используйте уравнение состояния, полученное разложением p на несколько рядов Тейлора T и xA (для 2-компонентных систем).) : П = п + — > — | г-а (г-т)+ — л(* А — * Л)+•= П-ПФ(Г-Т)- — Е («А-Л)+ — (17.33)) Где= = — (1 / p) (dr / dxA) m-величина ((J), а также определенная, которая указывает, как изменяется плотность при изменении composition.
В этом случае уравнение движения, если только гравитация является внешней силой, принимает форму П — ^ 7 — = — [в * М1-пите (ТМ) — АГ(1 Если концентрация в системе постоянна, то это выражение является формулой (10.29).Последний член уравнения (17.34) показывает «подъем», который происходит, когда средняя концентрация отклоняется от xA. Далее рассмотрим уравнение энергии. Возвращаясь к описанию чистой жидкости в разделе 10.1, напомним, что уравнение энергии может быть описано различными способами (функциями U, II или T).То же самое можно сказать и о смеси. Уравнение энергии (17.23) выражается функцией U +1/ gyR. Другие формы уравнений энергии приведены ниже.
Различные формы многих уравнений энергии / a * = 0, чтобы быть точным) (Обман) * Определение плотности теплового потока, содержащееся в этих уравнениях, описано в разделе 17.4. &+&=&+ 1 / для jv2: Людские ресурсы (XIII-3)* Заметим, что нет необходимости добавлять термин Sc для описания тепловой энергии, выделяющейся в ходе однородной химической реакции. Эта энергия неявно вводится в Y и U и точно отражается в представлении. Представительство»2ᵢHₗRₜ»или» 2ₗUₗRₗ»•(ХШ-е) и (ХШ-ж). Напомним, что при расчете H или d необходимо учитывать энергию образования и перемешивания различных компонентов смеси (см.
Смотрите также:

