Оглавление:
Уравнения с разделяющимися переменными
Наиболее простым ДУ первого порядка является, уравнение вида
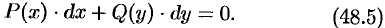
В нем одно слагаемое зависит только от 
, а другое — от 
. Иногда такие ДУ называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получаем:
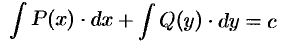
— его общий интеграл.
Пример №48.2.
Найти общий интеграл уравнения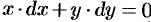 
.
Решение:
Данное уравнение есть ДУ с разделенными переменными.
Поэтому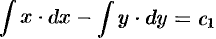 
или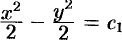 
. Обозначим 
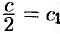. Тогда 
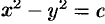— общий интеграл ДУ.
Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид
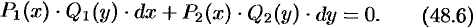
Особенность уравнения (48.6) в том, что коэффициенты пр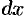и 
и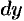 
представляют собой произведения двух функций (чисел), одна из которых зависит только от , другая — только от .
Уравнение (48.6) легко сводится к уравнению (48.5) путем почленного деления его на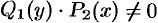 
. Получаем:
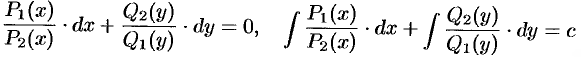
— общий интеграл.
Замечания. 1. При проведении почленного деления ДУ на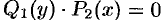 
могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение 
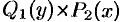и установить те решения ДУ, которые не могут быть получены из общего решения, — особые решения.
2. Уравнение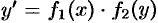 
также сводится к уравнению с разделенными переменными. Для этого достаточно положить 
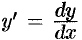и разделить переменные.
3. Уравнени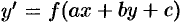е 
, где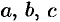 
— числа, путем замены 
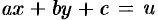сводится к ДУ с разделяющимися переменными. Дифференцируя по , получаем:
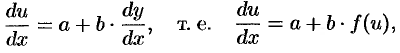
откуда следует
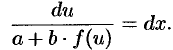
Интегрируя это уравнение и заменяя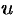 
на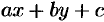 
, получим общий интеграл исходного уравнения.
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Наибольшее и наименьшее значения функции в замкнутой области |
| Задачи, приводящие к дифференциальным уравнениям |
| Однородные дифференциальные уравнения |
| Линейные уравнения Бернулли |
