Оглавление:
Уравнения, решаемые с помощью оценки их левой и правой частей. Уравнения, содержащие знаки корня и модуля
Справочные сведения
Оценка левой и правой части уравнения.
Решение некоторых тригонометрических уравнений основывается на неравенствах

Кроме этих неравенств могут оказаться полезными неравенства

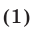
справедливые для любых 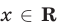 и для любых натуральных кип. Складывая неравенства (1), получаем
и для любых натуральных кип. Складывая неравенства (1), получаем
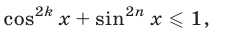
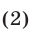
причем неравенство (2) является строгим при 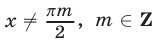
Если 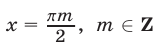 , то справедливо равенство
, то справедливо равенство
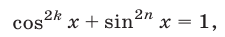
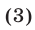
т. е. числа 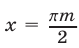 ,
, 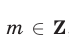 , и только они, являются корнями уравнения (3) при любых
, и только они, являются корнями уравнения (3) при любых 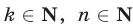 . Если уравнение имеет вид
. Если уравнение имеет вид
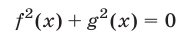
или преобразуется к такому виду, то оно равносильно системе уравнений
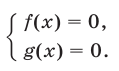
Уравнения, содержащие знак корня.
Если тригонометрическое уравнение имеет вид
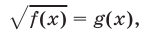
то, как было отмечено в §8, такое уравнение равносильно системе
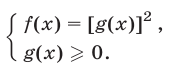
При решении тригонометрических уравнений вида
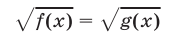
следует иметь в виду, что такое уравнение равносильно каждой из следующих систем:
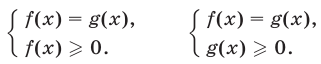
Уравнения, содержащие знак модуля.
При решении тригонометрических уравнений, содержащих знак модуля, следует иметь в виду, что
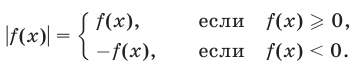
Примеры с решениями
Пример №137.
Решить уравнение 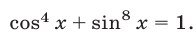
Решение:
В § 12 (см. пример 8) решение этого уравнения было получено с помощью подстановки 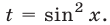 Данное уравнение — это уравнение вида (3) при
Данное уравнение — это уравнение вида (3) при 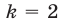 ,
, 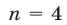 и поэтому его корнями являются числа
и поэтому его корнями являются числа 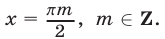
Ответ. 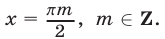
Пример №138.
Решить уравнение 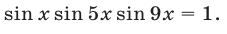
Решение:
Так как 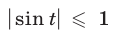 для любого
для любого 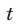 , то уравнение может иметь корни только в том случае, когда
, то уравнение может иметь корни только в том случае, когда 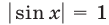 , т.е.
, т.е. 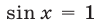 или
или 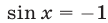 .
.
Если 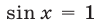 , то
, то 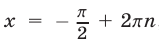 ,
, 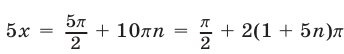 ,
, 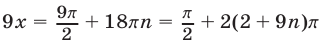 откуда
откуда 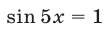 ,
, 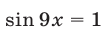 . Поэтому числа
. Поэтому числа 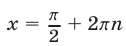 — корни данного уравнения.
— корни данного уравнения.
Если 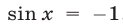 , то
, то 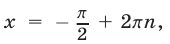
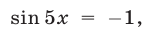
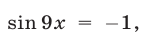
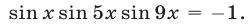 Поэтому корни уравнения
Поэтому корни уравнения 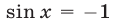 не являются корнями исходного уравнения.
не являются корнями исходного уравнения.
Ответ. 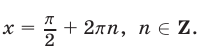
Пример №139.
Решить уравнение
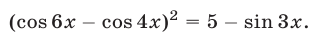
Решение:
Левая часть уравнения (4) не превосходит четырех, так как 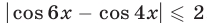 , а правая не меньше четырех. Отсюда следует, что уравнение (4) может иметь решения только при одновременном выполнении условий
, а правая не меньше четырех. Отсюда следует, что уравнение (4) может иметь решения только при одновременном выполнении условий
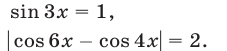
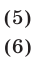
Если справедливо равенство (5), то
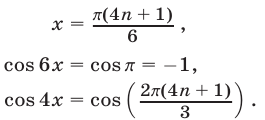
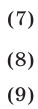
Из (8) и (9) следует, что равенство (6) верно только тогда, когда 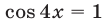 , т.е. когда число
, т.е. когда число 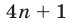 делится на 3. Число вида
делится на 3. Число вида 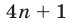 делится на 3 тогда и только тогда, когда
делится на 3 тогда и только тогда, когда 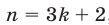 , где
, где 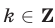 .
.
Ответ. 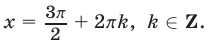
Пример №140.
Решить уравнение
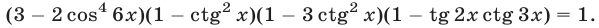
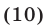
Решение:
Допустимые значения 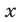 определяются условиями
определяются условиями

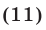
Воспользуемся равенствами
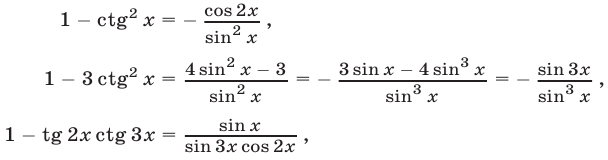
справедливыми при условиях (11).
Тогда уравнение (10) равносильно уравнению
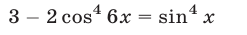
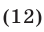
при выполнении условий (11).
Так как 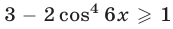 , a
, a 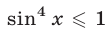 , то уравнение (12) равносильно системе уравнений
, то уравнение (12) равносильно системе уравнений
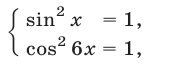
которая, в свою очередь, равносильна системе
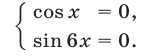
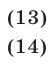
Поскольку каждый корень уравнения (13) является корнем уравнения (14), а для значений 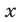 , удовлетворяющих уравнению (13), выполняются условия (11), уравнение (13) равносильно уравнению (10).
, удовлетворяющих уравнению (13), выполняются условия (11), уравнение (13) равносильно уравнению (10).
Ответ. 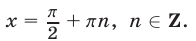
Пример №141.
Решить уравнение 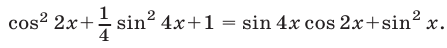
Решение:
Уравнение можно записать в виде
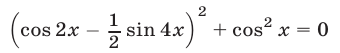
и поэтому оно равносильно системе
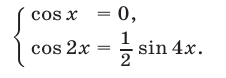
Уравнение 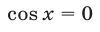 имеет корни
имеет корни 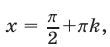 которые не являются корнями второго уравнения системы. Поэтому исходное уравнение не имеет корней.
которые не являются корнями второго уравнения системы. Поэтому исходное уравнение не имеет корней.
Пример №142.
Найти все корни уравнения
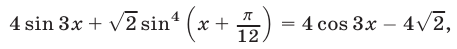
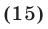
принадлежащие отрезку 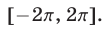
Решение:
Уравнение (15) равносильно каждому из следующих уравнений:
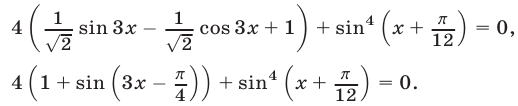
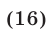
Уравнение (16) равносильно системе уравнений
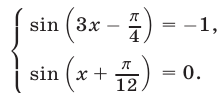
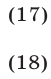
Из (18) следует, что
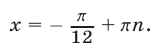
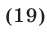
Подставляя найденное значение 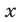 в уравнение (17), получаем
в уравнение (17), получаем
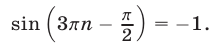
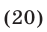
Равенство (20) является верным в том и только в том случае, когда 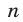 — четное число. Поэтому все корни уравнения (15) определяются формулой
— четное число. Поэтому все корни уравнения (15) определяются формулой
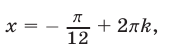
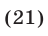
а отрезку 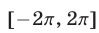 принадлежат те значения
принадлежат те значения 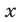 , которые получаются из формулы (21) при
, которые получаются из формулы (21) при 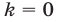 и
и 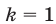 .
.
Ответ. 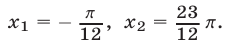
Пример №143.
Решить уравнение
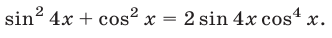
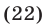
Решение:
Первый способ. Запишем уравнение в виде
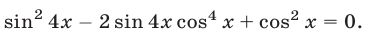
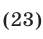
Прибавляя и вычитая в левой части уравнения (23) 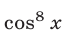 , преобразуем это уравнение к виду
, преобразуем это уравнение к виду
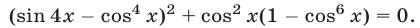
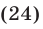
Равенство (24) является верным тогда и только тогда, когда верны равенства
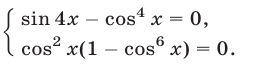
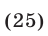
Система (25) равносильна совокупности двух систем
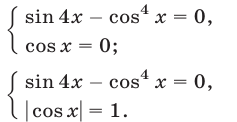
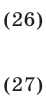
Если 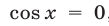 , то
, то 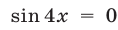 , и система (26) имеет решения
, и система (26) имеет решения 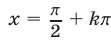 , которые являются решениями уравнения (22).
, которые являются решениями уравнения (22).
Система (27) не имеет решений, так как из равенства 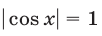 следует, что
следует, что 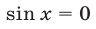 и
и 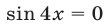 .
.
Ответ. 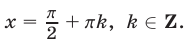
Второй способ. Решив уравнение (22) как квадратное относительно 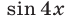 , получаем
, получаем
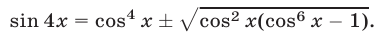
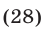
Из (28) следует, что уравнение (22) может иметь решение лишь тогда, когда 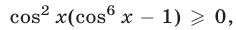 т.е. при условии, что хотя бы одно из равенств
т.е. при условии, что хотя бы одно из равенств 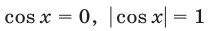 является верным.
является верным.
Если 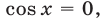 то из (28) получаем
то из (28) получаем 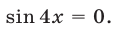 Числа
Числа 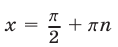 являются решениями уравнения (22). Если
являются решениями уравнения (22). Если 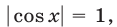 то
то 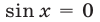 и
и 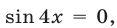 но из (28) следует, что
но из (28) следует, что 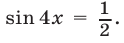 Итак, снова получаем, что числа
Итак, снова получаем, что числа 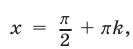 и только они, являются корнями уравнения (22).
и только они, являются корнями уравнения (22).
Пример №144.
Решить уравнение
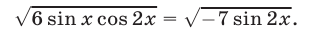
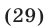
Решение:
Возведя обе части уравнения (29) в квадрат, получаем уравнение 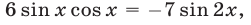 которое равносильно каждому из уравнений
которое равносильно каждому из уравнений
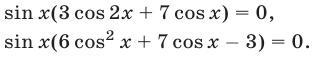
Уравнение 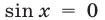 имеет корни
имеет корни 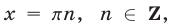 являющиеся корнями уравнения (29). Решив уравнение
являющиеся корнями уравнения (29). Решив уравнение 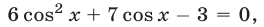 находим
находим 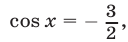
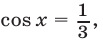 откуда
откуда
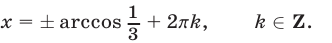
Из чисел, определяемых формулой (30), уравнению (29) удовлетворяют лишь те значения 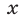 , для которых
, для которых 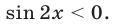
Так как 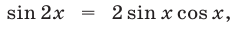 a
a 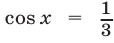 , то неравенство
, то неравенство 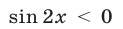 равносильно неравенству
равносильно неравенству 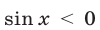 и поэтому в формуле (30) знак
и поэтому в формуле (30) знак 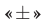 следует заменить на знак
следует заменить на знак 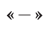 .
.
Ответ. 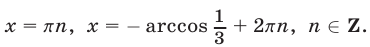
Пример №145.
Решить уравнение
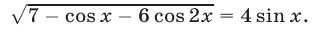
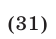
Решение:
Левая часть уравнения определена при всех значениях 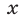 , так как
, так как 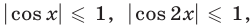 и неотрицательна. Возведя обе части уравнения (31) в квадрат, получим уравнение
и неотрицательна. Возведя обе части уравнения (31) в квадрат, получим уравнение
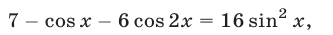
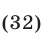
являющееся следствием уравнения (31).
Корнями уравнения (31) являются все те и только те корни уравнения (32), которые удовлетворяют условию
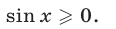

Иначе говоря, уравнение (31) равносильно системе, состоящей из уравнения (32) и неравенства (33).
Уравнение (32) сводится к квадратному относительно  , если воспользоваться формулой
, если воспользоваться формулой 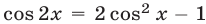 . Применив эту формулу, запишем уравнение (32) в виде
. Применив эту формулу, запишем уравнение (32) в виде 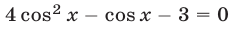 , откуда найдем
, откуда найдем 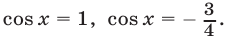
Если 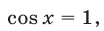 , то
, то 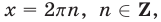 а условие (33) выполняется.
а условие (33) выполняется.
Если 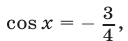 то
то
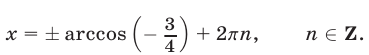
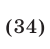
В том случае, когда в формуле (34) взят знак 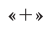 ,
, 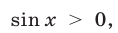 а если взят знак
а если взят знак 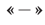 , то
, то 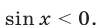
Отметим еще, что 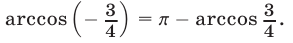
Ответ.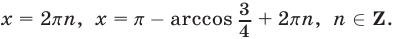
Замечание. Многие абитуриенты допустили ошибку, решая уравнение (32) без учета условия (33). Это привело к появлению посторонних для уравнения (31) корней.
Пример №146.
Решить уравнение
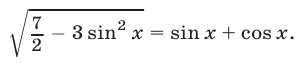
Решение:
Возведя обе части уравнения (35) в квадрат, получим уравнение
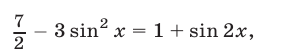
являющееся следствием уравнения (35). Уравнение (36) равносильно каждому из следующих уравнений:
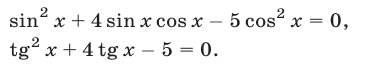
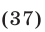
Решив уравнение (37), находим 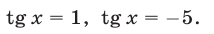
1) Если 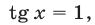 то
то
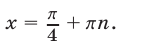
Пусть в формуле (38) 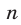 — четное число
— четное число 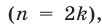 тогда числа
тогда числа 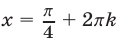 — корни уравнения (35), так как
— корни уравнения (35), так как 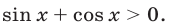
Пусть 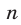 — нечетное число
— нечетное число 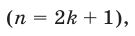 тогда
тогда
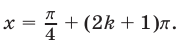
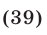
Из (39) следует, что 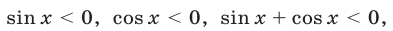 и поэтому значения
и поэтому значения 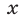 , определяемые формулой (39), не являются корнями уравнения (35).
, определяемые формулой (39), не являются корнями уравнения (35).
2) Если 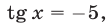 то
то
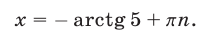
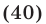
Пусть в формуле (40) 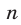 — четное число, тогда
— четное число, тогда
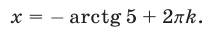
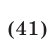
Положим 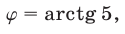 отсюда
отсюда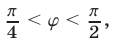
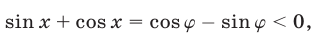 так как
так как 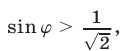
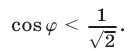 Поэтому значения
Поэтому значения 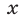 , определяемые формулой (41), не являются корнями уравнения (35).
, определяемые формулой (41), не являются корнями уравнения (35).
Пусть 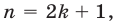 тогда числа
тогда числа 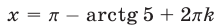 корни уравнения (35), поскольку в этом случае
корни уравнения (35), поскольку в этом случае 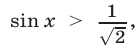
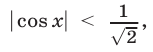
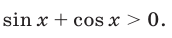
Ответ. 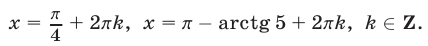
Пример №147.
Решить уравнение
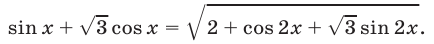
Решение:
Так как правая часть уравнения (42) неотрицательна, то уравнение может иметь решения только в том случае, когда
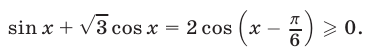
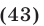
Если освободиться от радикала возведением обеих частей уравнения (42) в квадрат, то получается уравнение
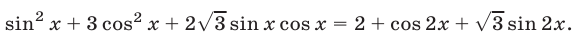
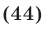
Уравнение (44) является тождеством. Однако это не означает, что уравнению (42) удовлетворяют все значения 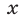 , поскольку уравнение (44) — лишь следствие уравнения (42). Эти уравнения равносильны при выполнении условия (43). Таким образом, решениями уравнения (42) являются все значения
, поскольку уравнение (44) — лишь следствие уравнения (42). Эти уравнения равносильны при выполнении условия (43). Таким образом, решениями уравнения (42) являются все значения 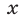 , удовлетворяющие неравенству (43), и только эти значения. Решая неравенство (43), получаем
, удовлетворяющие неравенству (43), и только эти значения. Решая неравенство (43), получаем
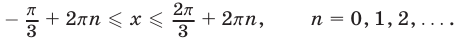
Ответ. Объединение всех отрезков вида
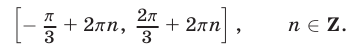
Замечание. Так как
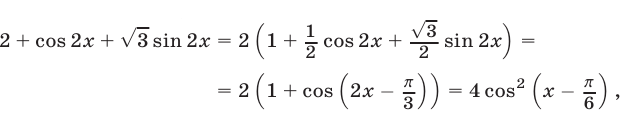
то уравнение (42) равносильно уравнению
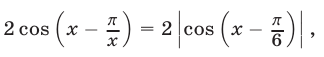
решениями которого являются те и только те значения х, которые удовлетворяют неравенству 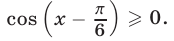
Пример №148.
Решить уравнение
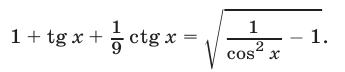
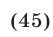
Решение:
Допустимые значения 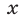 определяются условием
определяются условием 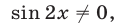 а уравнение (45) можно записать в виде
а уравнение (45) можно записать в виде
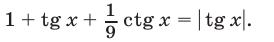
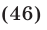
Рассмотрим два случая: 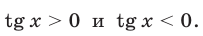
1) Если 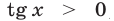 , то уравнение (46) приводится к виду
, то уравнение (46) приводится к виду 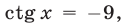 откуда следует, что
откуда следует, что 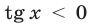 . В данном случае решений нет.
. В данном случае решений нет.
2) Если 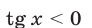 , то, полагая в (46)
, то, полагая в (46) 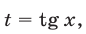 получаем
получаем
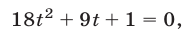
откуда 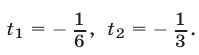
Ответ. 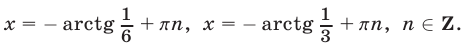
Пример №149.
Решить уравнение
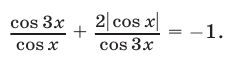
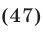
Решение:
Положим 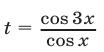 рассмотрим два возможных случая:
рассмотрим два возможных случая:
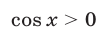 и
и 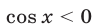
а) Пусть 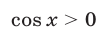 , тогда уравнение (47) примет вид
, тогда уравнение (47) примет вид
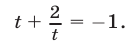

Уравнение (48), равносильное уравнению (47), не имеет действительных корней.
б) Пусть 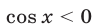 , тогда уравнение (47) примет вид
, тогда уравнение (47) примет вид
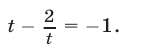
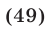
Так как 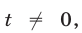 то уравнение (49), равносильное уравнению
то уравнение (49), равносильное уравнению 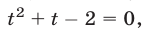 имеет корни
имеет корни 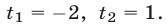
Если  то
то
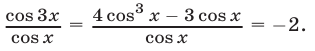
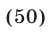
Так как 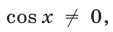
, то уравнение (50) равносильно уравнению 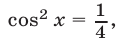 откуда, с учетом условия
откуда, с учетом условия 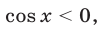 получаем
получаем 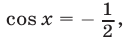
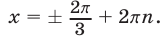
Если 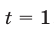 , то
, то 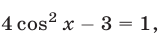
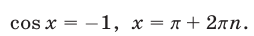
Ответ.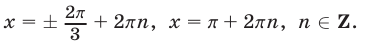
Пример 150.
Решить уравнение
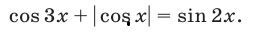
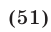
Решение:
Возможны два случая: 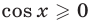 и
и 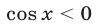 .
.
1) Пусть 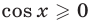 , тогда уравнение (51) примет вид
, тогда уравнение (51) примет вид
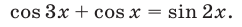
Преобразуя это уравнение, получаем
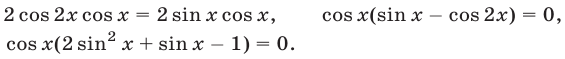
Если 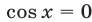 , то
, то
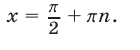
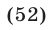
Если 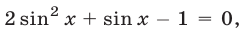
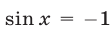 или
или 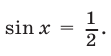
Корни уравнения 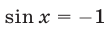 содержатся в серии (52).
содержатся в серии (52).
Решив уравнение 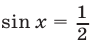 с учетом условия
с учетом условия 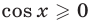 , находим
, находим
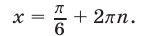
2) Пусть 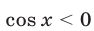 , тогда из (51) следует, что
, тогда из (51) следует, что

Решив уравнения 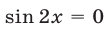 и
и 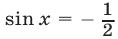 при условии
при условии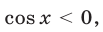 найдем еще две серии корней уравнения (51):
найдем еще две серии корней уравнения (51):
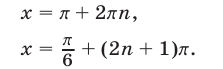

Серии (53) и (55) можно объединить в одну: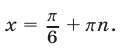
Ответ. 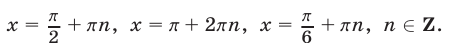
Пример №151.
Решить уравнение
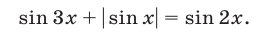
Решение:
Рассмотрим два случая: 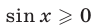 и
и 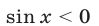 .
.
1) Если 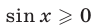 , то
, то 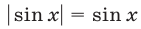 и уравнение (56) равносильно каждому из уравнений
и уравнение (56) равносильно каждому из уравнений
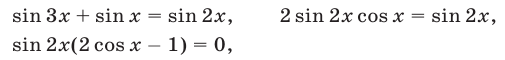
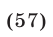
а уравнение (57) равносильно совокупности уравнений
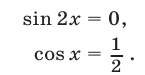
Условию 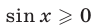 удовлетворяют следующие две серии корней уравнения (58):
удовлетворяют следующие две серии корней уравнения (58):
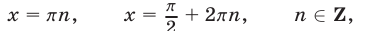
а также корни уравнения (59) такие, что
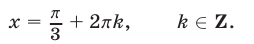
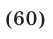
2) Если 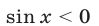 , то
, то 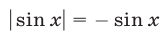 и уравнение (56) равносильно каждому из уравнений
и уравнение (56) равносильно каждому из уравнений
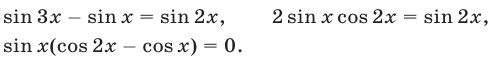
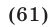
Так как 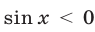 , то уравнение (61) равносильно каждому из уравнений
, то уравнение (61) равносильно каждому из уравнений
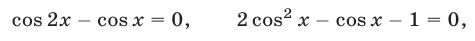
откуда получаем 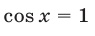 (и тогда
(и тогда 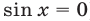 ) и
) и
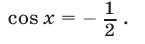
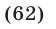
Таким образом, если 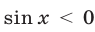 , то все корни уравнения (56) содержатся среди корней уравнения (62), т. е. среди чисел вида
, то все корни уравнения (56) содержатся среди корней уравнения (62), т. е. среди чисел вида
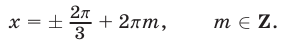
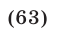
Условию 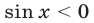 удовлетворяют числа из формулы (63), взятые со знаком
удовлетворяют числа из формулы (63), взятые со знаком 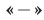 , т. е. значения
, т. е. значения
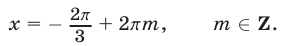
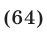
Заметим, что серии (64) и (60) можно объединить в одну: 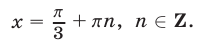
Ответ. 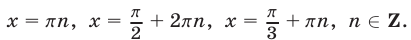
Пример №152.
Решить уравнение
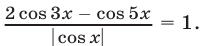
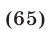
Решение:
Здесь ОДЗ уравнения (65) определяется условием 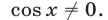 Рассмотрим два возможных случая:
Рассмотрим два возможных случая: 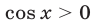 и
и 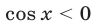 .
.
1) Если 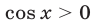 , то все корни уравнения (65) содержатся среди корней каждого из следующих равносильных уравнений:
, то все корни уравнения (65) содержатся среди корней каждого из следующих равносильных уравнений:
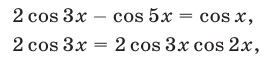
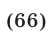
а уравнение (66) равносильно совокупности уравнений
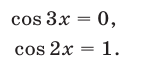
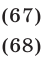
Чтобы найти корни уравнения (67), удовлетворяющие условию 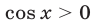 , воспользуемся формулой
, воспользуемся формулой
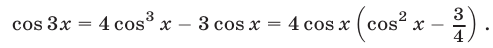
Отсюда следует, что уравнению (67) и условию 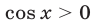 удовлетворяют корни уравнения
удовлетворяют корни уравнения 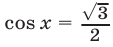 т.е. числа
т.е. числа
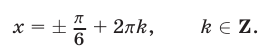
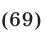
Корнями уравнения (68), удовлетворяющими условию 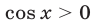 , являются числа
, являются числа
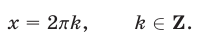
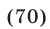
2) Если 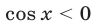 , то все корни уравнения (65) содержатся среди корней каждого из следующих уравнений:
, то все корни уравнения (65) содержатся среди корней каждого из следующих уравнений:
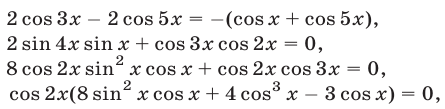
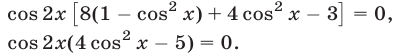
Уравнение 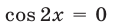 равносильно уравнению
равносильно уравнению 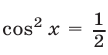 , откуда (при условии
, откуда (при условии 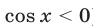 )
) 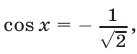
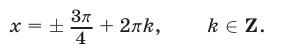
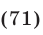
Уравнение 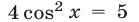 не имеет корней. Таким образом, корнями уравнения (65) являются числа, определяемые формулами (69)—(71).
не имеет корней. Таким образом, корнями уравнения (65) являются числа, определяемые формулами (69)—(71).
Ответ. 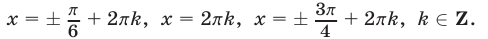
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

