Оглавление:
Уравнения равновесия плоской системы параллельных сил
Так как параллельное расположение сил на плоскости является частным случаем их произвольного на ней расположения, то к такой системе также могут быть применены установленные в предыдущем параграфе три уравнения равновесия плоской системы сил:
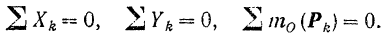
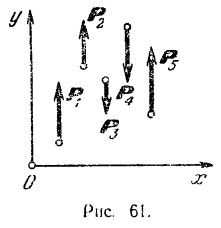
Пользуясь тем, что оси проекций можно располагать в плоскости действия сил как угодно, проведем ось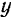 
параллельно данным силам, а ось 
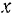— перпендикулярно к ним (рис. 61).
Проекция каждой из сил на ось 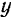будет равна нулю, и потому первое из уравнении обращается в тождество при любых значениях сил. Следовательно, уравнение 
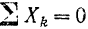выполняется для системы параллельных сил, независимо от того, находится ли эта система в равновесии или нет.
Так как все данные силы параллельны оси 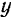, то сумма проекций этих сил на ось 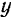равна сумме модулей этих сил, взятых со знаком плюс, когда они направлены в одну какую-либо сторону, и со знаком минус, когда они направлены в противоположную сторону:
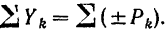
Для простоты будем в дальнейшем обозначать эту сумму просто
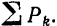
Таким образом, уравнения равновесия для плоской системы параллельных сил принимают вид
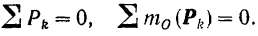
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы порознь равнялись нулю алгебраическая сумма всех сил и сумма алгебраических величин моментов всех сил относительно любой точки, лежащей в плоскости действия сил.
Вспоминая сказанное на стр. 83 о третьей возможной форме уравнении равновесия плоской системы сил (уравнения (28)), уравнениям равновесия плоской системы параллельных сил можно придать другую форму.
Направим ось 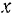перпендикулярно параллельным силам. Тогда уравнение
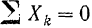
обращается о тождество и отпадает.
Остаются два уравнения
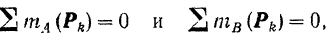
причем центры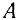 
и 
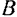моментов должны быть выбраны так, чтобы ось 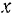была не перпендикулярна прямой 
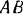, т. е. чтобы точк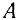и и 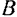не лежали на прямой, параллельной данным силам.
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы порознь равнялись нулю суммы алгебраических величин моментов всех сил относительно каждой из двух произвольно выбранных, но не лежащих на прямой, параллельной данным силам, точек плоскости:
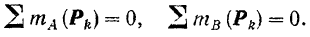
Пример задачи:
На двухконсольную горизонтальную балку действует пара сил с моментом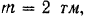 
, на правую консоль — равномерно распределенная нагрузка интенсивностью 
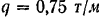, а в точке 
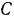левой консоли — вертикальная сосредоточенная нагрузка 
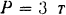. Размеры балки указаны на чертеже (рис. 62). Определить реакции опор 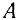и .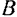
Решение:
Для определения реакций опор заменим распределенную нагрузку, действующую на участке балки длиной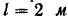 
, равнодействующей. Так как нагрузка равномерно распределена по всей длине участка, то ее равнодействующая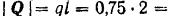 
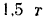приложена в точке 
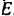, середине участка 
.
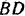Реакция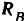 
подвижной опоры и приложенные к балке активные силы 
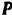и 
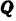вертикальны. Так как пара сил может только вращать тело и не может сообщить балке горизонтального перемещения, то реакция 
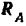неподвижной опоры 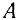будет направлена также вертикально.
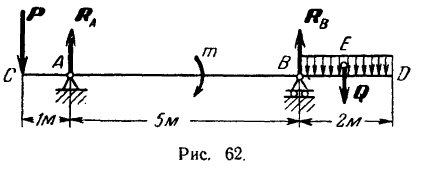
Составляем уравнения (30) равновесия балки. Так как (стр. 74) сумма алгебраических величии моментов сил пары относительно любого центра равна моменту пары и данная пара вращает плоскость чертежа по часовой стрелке, то
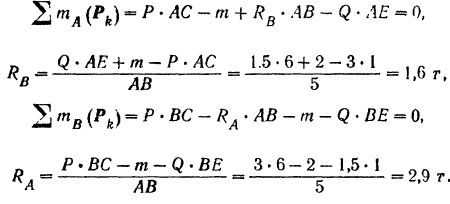
Полученный результат можно проверить. Так как балка находится в равновесии, то уравнение
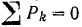
должно обращаться при подстановке в него значений приложенных к балке сил в тождество. Действительно,
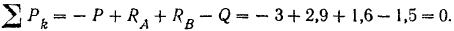
Силы пары в это уравнение мы не подставляем, так как алгебраическая сумма их всегда равна нулю.
Пример задачи:
Балка заложена в стену на глубину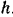 
Длина выступающей части балки равна 
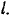Пренебрегая весом балки определить реакции стены в точках 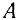и 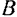(рис. 63), если к свободному концу балки подвешен груз 
.
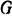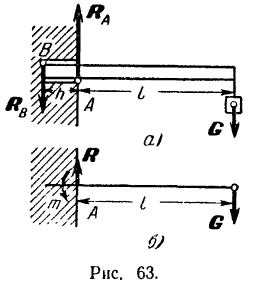
Решение:
Как видно из рис. 63, а, приложенная к балке сила 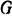стремится повернуть се так, чтобы давление балки на стену в точке А было направлено вертикально вниз, а потому реакция 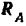стены в этой точке направлена вертикально вверх; давление же балки па стену в точке 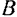направлено вертикально вверх и, следовательно, реакция 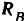стены в точке 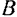направлена вертикально вниз.
Составляя уравнения (30) равновесия для плоской системы параллельных сил, будем иметь:
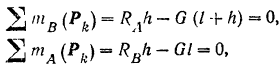
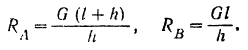
Найденным реакциям стены в месте заделки можно придать и другую (рис. 63,6), часто применяемую форму, о которой было сказано выше (стр. 85). Так как
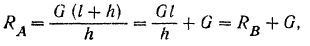
то реакцию 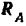можно разложить на две составляющие 
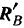и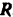 
, направленные по линии действия силы 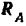в ту же сторону и равные по модулю
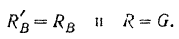
Силы 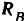и 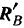образуют пару. Момент этой пары
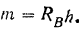
Этот момент, как видно из уравнения (II), равен но абсолютной величине моменту активной силы 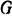, приложенной к балке, относительно точки опоры :
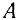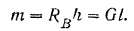
Он уравновешивает вращательный эффект приложенной к балке активной силы, т. е. препятствует вращению балки. Как видно из предыдущего равенства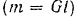 
, он не зависит от глубины заделки белки.
Реакция 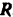, равная по модулю приложенной к балке активной силе и направленная в противоположную ей сторону, делает невозможным поступательное движение балки.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
