Уравнения равновесия Лагранжа
По определению (18.3) обобщенные силы
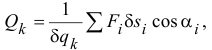
при 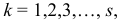 где
где 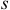 — число степеней свободы.
— число степеней свободы.
Если система находится в равновесии, то по принципу возможных премещений (17.1)
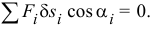
Здесь 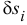 — перемещения, допускаемые связями, возможные перемещения. Поэтому при равновесии материальной системы все её обобщенные силы равны нулю
— перемещения, допускаемые связями, возможные перемещения. Поэтому при равновесии материальной системы все её обобщенные силы равны нулю
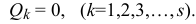
Эти уравнения, уравнения равновесия в обобщенных координатах, или уравнения равновесия Лагранжа, позволяют решать задачи статики еще одним методом.
Если система консервативная, то
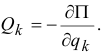
Значит, в положении равновесия
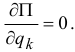
То есть в положении равновесия такой материальной системы ее потенциальная энергия либо максимальна, либо минимальна, то есть функция 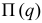 имеет экстремум.
имеет экстремум.
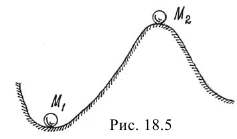
Это очевидно из анализа простейшего примера (рис. 18.5). Потенциальная энергия шарика в положении 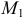 имеет минимум, в положении
имеет минимум, в положении 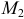 — максимум. Можно заметить, что в положении
— максимум. Можно заметить, что в положении 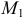 равновесие будет устойчивым; в положении
равновесие будет устойчивым; в положении  — неустойчивым.
— неустойчивым.
Равновесие считается устойчивым, если телу в этом положении сообщить малую скорость или сместить на малое расстояние, то эти отклонения в дальнейшем не увеличатся.
Можно доказать (теорема Лагранжа-Дирихле), что если в положении равновесия консервативной системы ее потенциальная энергия имеет минимум, то это положение равновесия устойчиво.
Для консервативной системы с одной степенью свободы условие минимума потенциальной энергии, а значит и устойчивости положения равновесия, определяется второй производной, ее значением в положении равновесия
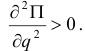
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Обобщенные координаты в теоретической механике |
| Обобщенные силы |
| Обобщенные силы инерции в теоретической механике |
| Теорема о движении центра масс |

