Оглавление:
Уравнения прямой в пространстве
Векторное уравнение прямой
Положение прямой в пространстве вполне определено, если задать какую-либо точку 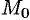 на прямой и вектор
на прямой и вектор 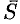 , параллельный этой прямой. Вектор
, параллельный этой прямой. Вектор 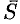 называется направляющим вектором прямой. Пусть прямая
называется направляющим вектором прямой. Пусть прямая  задана ее точкой
задана ее точкой 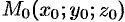 и направляющим вектором
и направляющим вектором 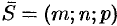 . Возьмем на прямой
. Возьмем на прямой  произвольную точку
произвольную точку 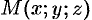 . Обозначим радиус-векторы точек
. Обозначим радиус-векторы точек 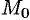 и
и 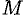 соответственно через
соответственно через 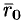 и
и  . Очевидно, что три вектора
. Очевидно, что три вектора 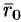 ,
,  и
и 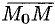 связаны соотношением
связаны соотношением

Вектор 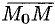 , лежащий на прямой
, лежащий на прямой  , параллелен направляющему вектору
, параллелен направляющему вектору 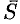 , поэтому
, поэтому 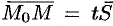 , где
, где 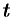 — скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки
— скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки 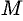 на прямой (см. рис. 75).
на прямой (см. рис. 75).
Уравнение (12.10) можно записать в виде

Полученное уравнение называется векторным уравнением прямой.
Параметрические уравнения прямой
Замечая, что 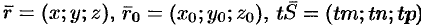 , уравнение (12.11) можно записать в виде
, уравнение (12.11) можно записать в виде
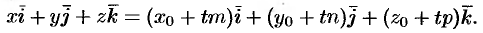
Отсюда следуют равенства:

Они называются параметрическими уравнениями прямой в пространстве.
Канонические уравнения прямой
Пусть 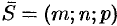 — направляющий вектор прямой
— направляющий вектор прямой  и
и 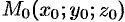 — точка, лежащая на этой прямой. Вектор
— точка, лежащая на этой прямой. Вектор 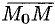 , соединяющий точку
, соединяющий точку 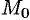 с произвольной точкой
с произвольной точкой 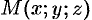 прямой
прямой  , параллелен вектору
, параллелен вектору 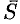 . Поэтому координаты вектора
. Поэтому координаты вектора 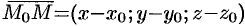 и вектора
и вектора 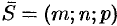 пропорциональны:
пропорциональны:
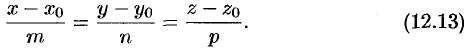
Уравнения (12.13) называются каноническими уравнениями прямой в пространстве.
Замечания: 1) Уравнения (12.13) можно было бы получить сразу из параметрических уравнений прямой (12.12), исключив параметр 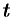 . Из уравнений (12.12) находим
. Из уравнений (12.12) находим
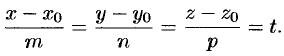
2) Обращение в нуль одного из знаменателей уравнений (12.13) означает обращение в нуль соответствующего числителя.
Например, уравнения 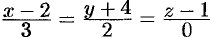 задают прямую, про-
задают прямую, про-
ходящую через точку 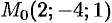 перпендикулярно оси
перпендикулярно оси 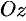 (проекция вектора
(проекция вектора 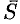 на ось
на ось 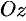 равна нулю). Но это означает, что прямая лежит в плоскости
равна нулю). Но это означает, что прямая лежит в плоскости 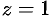 , и поэтому для всех точек прямой будет
, и поэтому для всех точек прямой будет 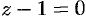 .
.
Уравнение прямой в пространстве, проходящей через две точки
Пусть прямая  проходит через точки
проходит через точки 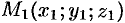 и
и 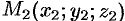 . В качестве направляющего вектора
. В качестве направляющего вектора 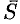 можно взять вектор
можно взять вектор 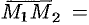
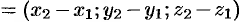 , т.е.
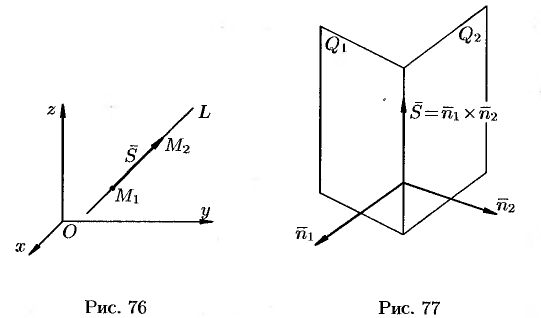
, т.е. 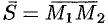 (см. рис. 76). Следовательно,
(см. рис. 76). Следовательно, 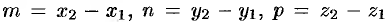 . Поскольку прямая проходит через точку
. Поскольку прямая проходит через точку 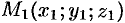 , то, согласно уравнениям (12.13), уравнения прямой
, то, согласно уравнениям (12.13), уравнения прямой  имеют вид
имеют вид
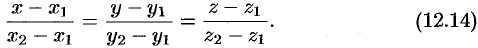
Уравнения (12.14) называются уравнениями прямой, проходящей через две данные точки.
Общие уравнения прямой
Прямую в пространстве можно задать как линию пересечения двух не параллельных плоскостей. Рассмотрим систему уравнений
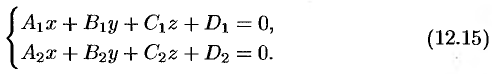
Каждое из уравнений этой системы определяет плоскость. Если плоскости не параллельны (координаты векторов 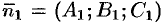 и
и 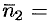
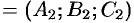 не пропорциональны), то система (12.15) определяет прямую
не пропорциональны), то система (12.15) определяет прямую  как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы (см. рис. 77). Уравнения (12.15) называют общими уравнениями прямой.
как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы (см. рис. 77). Уравнения (12.15) называют общими уравнениями прямой.
От общих уравнений (12.15) можно перейти к каноническим уравнениям (12.13). Координаты точки 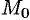 па прямой
па прямой  получаем из системы уравнений (12.15), придав одной из координат произвольное значение (например,
получаем из системы уравнений (12.15), придав одной из координат произвольное значение (например, 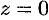 ).
).
Так как прямая  перпендикулярна векторам
перпендикулярна векторам 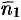 и
и 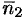 , то за направляющий вектор
, то за направляющий вектор 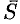 прямой
прямой  можно принять векторное произведение
можно принять векторное произведение
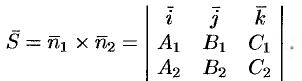
Замечание: Канонические уравнения прямой легко получить, взяв две какие-либо точки на пей и применив уравнения (12.14).
Пример №12.1.
Написать канонические уравнения прямой  , заданной уравнениями
, заданной уравнениями
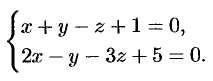
Решение:
Положим 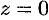 и решим систему
и решим систему 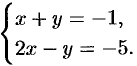 Находим точку
Находим точку 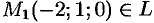 . Положим
. Положим 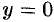 и решим систему
и решим систему 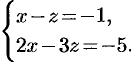 . Находим вторую точку
. Находим вторую точку 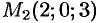 прямой
прямой  . Записываем уравнение прямой
. Записываем уравнение прямой  , проходящей через точки
, проходящей через точки 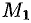 и
и 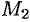 :
:
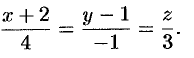
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Общее уравнение линий второго порядка |
| Плоскость. Основные задачи |
| Прямая линия в пространстве |
| Прямая и плоскость в пространстве |

