На плоскости с заданной декартовой системой координат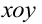 
положение прямой линии можно задать различными способами. Соответственно существуют различные уравнения прямой на плоскости. От одного вида уравнения можно перейти к другому.
1. Общее уравнение прямой:
Коэффициенты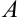 
, 
одновременно являются координатами вектора нормали к прямой 
.
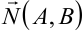2. Уравнение прямой с угловым коэффициентом:
3. Уравнение прямой, проходящей через заданную точку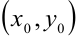 
с угловым коэффициентом:
4. Уравнение прямой, проходящей через заданную точку 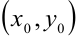перпендикулярно вектору :
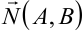5. Уравнение прямой, проходящей через две заданные точки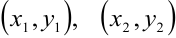 
:
6. Уравнение прямой, проходящей через заданную точку 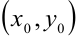параллельно вектору 
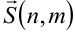(вектор 
называется направляющим вектором):
7. Уравнение прямой в отрезках:
Здесь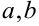 
— отрезки, отсечённые прямой на осях 
, 
.
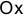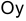Пусть заданы две прямые уравнениями
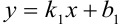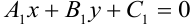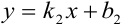или 
,
или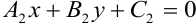 
.
Условия параллельности прямых:
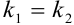или 
Условия перпендикулярности прямых:
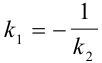или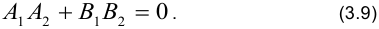 
Расстояние от точки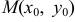 
до прямой 
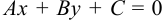находится по формуле: 
.
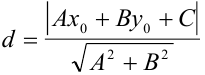Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Векторное произведение векторов: определение и пример с решением |
| Смешанное произведение трёх векторов: определение и пример с решением |
| Уравнения плоскости в пространстве |
| Эллипс, гипербола, парабола |
