Оглавление:
Уравнения плоскости в пространстве
Простейшей поверхностью является плоскость. Плоскость в пространстве 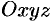 можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.
можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
Пусть в пространстве 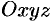 плоскость
плоскость  задана точкой
задана точкой 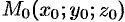 и вектором
и вектором 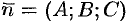 , перпендикулярным этой плоскости (см. рис. 69). Выведем уравнение плоскости
, перпендикулярным этой плоскости (см. рис. 69). Выведем уравнение плоскости 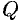 . Возьмем на ней произвольную точку
. Возьмем на ней произвольную точку 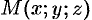 и составим вектор
и составим вектор
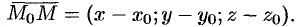
При любом расположении точки 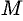 на плоскости
на плоскости 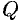 векторы
векторы 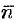 и
и 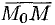 взаимно перпендикулярны, поэтому их скалярное произведение равно нулю:
взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: 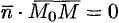 , т. е.
, т. е.
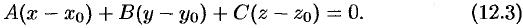
Координаты любой точки плоскости 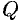 удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости
удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости 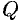 , этому уравнению не удовлетворяют (для них
, этому уравнению не удовлетворяют (для них 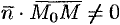 ).
).
Уравнение (12.3) называется уравнением плоскости, проходящей через данную точку 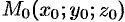 перпендикулярно вектору
перпендикулярно вектору 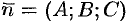 . Оно первой степени относительно текущих координат
. Оно первой степени относительно текущих координат 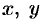 и
и 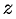 . Вектор
. Вектор 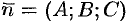 называется нормальным вектором плоскости.
называется нормальным вектором плоскости.
Придавая коэффициентам 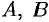 и
и 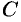 уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей через точку
уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей через точку 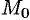 . Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей, а уравнение (12.3) — уравнением связки плоскостей.
. Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей, а уравнение (12.3) — уравнением связки плоскостей.
Общее уравнение плоскости
Рассмотрим общее уравнение первой степени с тремя переменными 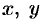 и
и 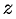 :
:
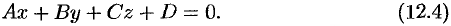
Полагая, что по крайней мере один из коэффициентов 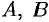 или
или 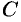 не равен нулю, например
не равен нулю, например 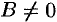 , перепишем уравнение (12.4) в виде
, перепишем уравнение (12.4) в виде
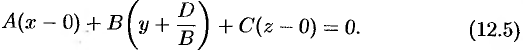
Сравнивая уравнение (12.5) с уравнением (12.3), видим, что уравнения (12.4) и (12.5) являются уравнением плоскости с нормальным вектором 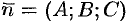 , проходящей через точку
, проходящей через точку 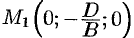 .
.
Итак, уравнение (12.4) определяет в системе координат  некоторую плоскость. Уравнение (12.4) называется общим уравнением плоскости.
некоторую плоскость. Уравнение (12.4) называется общим уравнением плоскости.
Частные случаи общего уравнения плоскости:
- Если
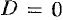 , то оно принимает вид
, то оно принимает вид 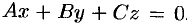 . Этому уравнению удовлетворяет точка
. Этому уравнению удовлетворяет точка 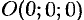 . Следовательно, в этом случае плоскость проходит через начало координат.
. Следовательно, в этом случае плоскость проходит через начало координат. - Если
 , то имеем уравнение
, то имеем уравнение 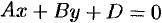 . Нормальный вектор
. Нормальный вектор 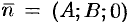 перпендикулярен оси
перпендикулярен оси 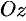 . Следовательно, плоскость параллельна оси
. Следовательно, плоскость параллельна оси 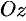 ; если
; если 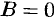 — параллельна оси
— параллельна оси 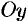 ,
, 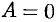 — параллельна оси
— параллельна оси 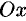 .
. - Если
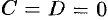 , то плоскость проходит через
, то плоскость проходит через 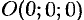 параллельно оси
параллельно оси 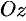 , т. е. плоскость
, т. е. плоскость 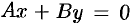 проходит через ось
проходит через ось 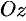 . Аналогично, уравнениям
. Аналогично, уравнениям 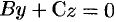 и
и 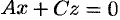 отвечают плоскости, проходящие соответственно через оси
отвечают плоскости, проходящие соответственно через оси 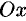 и
и 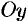 .
. - Если
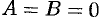 , то уравнение (12.4) принимает вид
, то уравнение (12.4) принимает вид 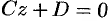 , т. е.
, т. е. 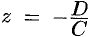 . Плоскость параллельна плоскости
. Плоскость параллельна плоскости  . Аналогично, уравнениям
. Аналогично, уравнениям 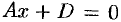 и
и 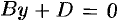 отвечают плоскости, соответственно параллельные плоскостям
отвечают плоскости, соответственно параллельные плоскостям 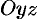 и
и 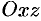 .
. - Если
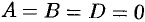 , то уравнение (12.4) примет вид
, то уравнение (12.4) примет вид 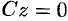 , т. е.
, т. е. 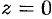 . Это уравнение плоскости
. Это уравнение плоскости 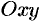 . Аналогично:
. Аналогично: 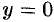 — уравнение плоскости
— уравнение плоскости 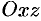 ;
; 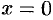 — уравнение плоскости
— уравнение плоскости 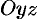 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Решение систем линейных уравнений методом Гаусса |
| Уравнения поверхности в пространстве |
| Числовые последовательности |
| Предел функции в точке |

