Уравнения плоского движения твердого тела. Уравнения движения точки плоской фигуры

Уравнения плоского движения твердого тела. Уравнения движения точки плоской фигуры

• Уравнение плоского движения твердого тела. Уравнения движения точек в плане этажа 1 Определите плоские уравнения движения твердого тела и плоские точки F и r движения. Плоскость (плоскопараллельная) — это движение последней цели, и траектория всех ее точек находится в плоскости, параллельной некоторой неподвижной плоскости. С этим ходом Все точки твердого тела, лежащие на приподнятом перпендикуляре к этой плоскости, имеют одинаковую траекторию, скорость и ускорение.

Поэтому при изучении плоского движения твердых тел достаточно изучить движение плоской фигуры. Движение плоской фигуры можно разложить на поступательное движение вместе с произвольно выбранной точки 0 [}, называемой полюсом, и вращение фигуры вокруг этой точки(рис. 6.1).

Плоская фигура-это сечение твердого грунта плоскостью, параллельной неподвижному грунту. Людмила Фирмаль

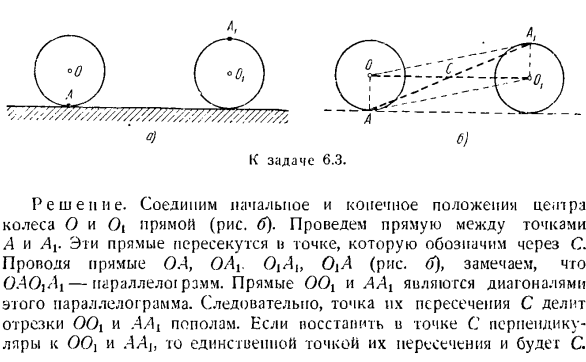
О Система координат, в которой находится уравнение Выберите фиксированные системы координат xy и nat и подключитесь строго к плану. Плоское движение твердого тела： xoi = Ф \ второй)> йот = л(0″ 9 = Дж.* И Х / г \ ч. 1. 1 Дж. 1 1-й- Рисунок 6.1. О) 0） К задаче 6.3. Решение. Соедините центр o колеса и начальное и конечное положения 0{прямая линия (рисунок B).Нарисуйте линию между точками A и Ax. Эти линии пересекаются и становятся точками, обозначенными C. OA, OAj. OiAh 0 \ A (рисунок Tf), a} a {- параллелограмм.

Прямые OOt и AAX являются диагоналями этого parallelogram. As в результате их пересечение C делит отрезки 00 \и AA {пополам. Если восстановить точки перпендикулярно к]и AA \в точках C, то единственной точкой их пересечения будет C. Таким образом, C является центром конечного вращения при перемещении колеса из первого положения во 2-е положение.

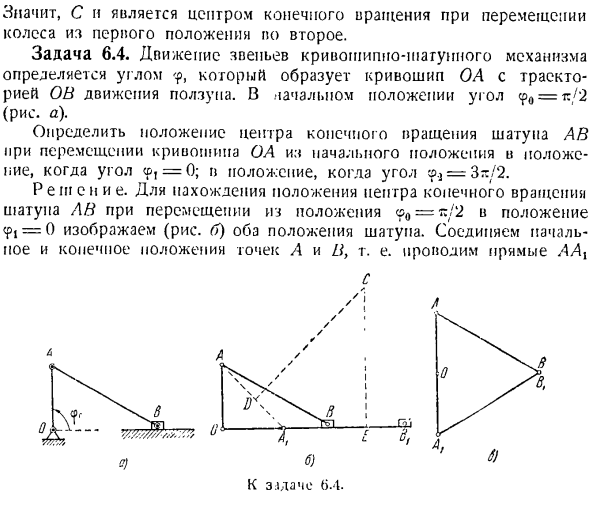
• Задача 6.4.Движение звена кривошипно-шагового механизма определяется углом, — [ — ’<] с COS <Р-СР МВ, г = yolJ7 Мп? «!» В этих уравнениях x, y-координаты точки M и фиксированная система координат. hoch> J’o, — координаты полюса O;; x, y {система координат X {y \координаты точки M, плотно связанной с плоской фигурой. 9-угол поворота подвижной системы координат. вый\, внизу константа, не меняется, но это время движения числа, которое определяет точку с учетом плоской фшуры. Оставшаяся сумма Формулы (2*) является функцией времени и определяется по центральной формуле

Задача 6.1.In кривошипно-шатунный механизм, центр вращения кривошипа О находится на расстоянии а от горизонтальной траектории ползуна В. угол поворота кривошипа изменяется по закону. 0 = hi, где k-постоянный / пятый коэффициент. Длина Кривошип () A = g, шатун AB-L О11 с треском замахнулся на меня плоско-плоскостным кругом движения на шатуне.

Поэтому точка а шатуна(начало координат движущейся системы координат) является полюсом. Людмила Фирмаль

К задаче 0.1. D e n c e. выберите 11C в качестве координаты координаты с точкой O в качестве начала координат. Возьмем начальную точку и движущуюся систему координат, содержащую точку А, которая принадлежит как кривошипу, так и Шатуну. .нарисуйте вдоль оси v, шатуна AB, оси y, перпендикулярно ей.

Форма уравнения движения полюсов имеет вид ХЛ = ОА что-то J = р потому что КТ, я = ОА грех или грех ХТ. Спроектировать отрезок AN по оси y, чтобы найти 3-е уравнение движения, то есть временную зависимость угла поворота шатуна. углы между j-осями обозначаются цифрой 9 ми » ж И Л -, найти： An sin 9 = OA sinO — ’ * а、 Или AN=/, OA = r, O-kt, так что это выглядит так: г. и… Фундамент? = 7 грехов?/-;- Отсюда возникает угол o как функция времени.

Задача 6.2.Жесткий прямой угол / GC перемещается так, что точка A всегда остается на оси y! Когда противоположная сторона угла L1C проходит через неподвижную точку N, мы знаем, что это AM-OH = a и определяем траекторию движения точки M. The solution. To определите траекторию движения точки M, выберите ту систему координат, которая начинается с точки N. укажите радиус К выпуску 62.

Вектор VM через r и угол OBM через a、 Я грех-Ф-БМ потому что = Обь、 Или грех Г, потому что А-А. Г. я-Силл А. И потому что а-р -» а-1•(•sifl Р (1) от： Или г 1-л грех «» л г _ ы ы а-1-зта г 1-СМЭВ в Отсюда, после простого преобразования, это выглядит так: _ * ля а + — р-2- Это уравнение траектории точки / и-станоид полярного координатного уравнения. 2°.Определение местоположения центра конечной плоскости плоского фщ-ИПУ.

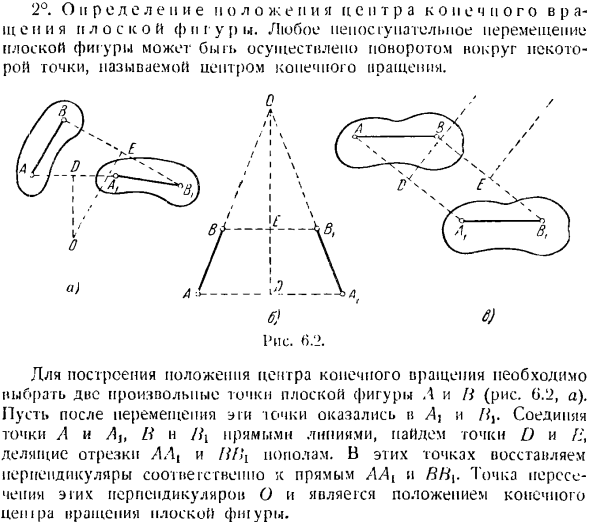
Прерывистые движения плоских фигур могут быть выполнены вращением вокруг точки, называемой центром конечного вращения. Да. 6.} Рисунок. >’_>. Чтобы построить положение центра конечного вращения, нужно выбрать любые 2 точки плоскости фигур а и Н(рис.6.！2, а).После перемещения этих точек мы находимся в точке Aj, и если соединить точки A и Ait Hn прямой линией, то будем считать, что точки D и f найдены.

Восстановление в этих точках АА {и ББ {.Точкой пересечения этих перпендикуляров O является положение последнего Петера при повороте вида в плане. Структура не ведет к цели только в том случае, если 2-я позиция плоской фигуры является зеркальным отражением первой фигуры(рис.6.2, б).Это связано с тем, что перпендикуляр, расположенный в середине сегментов LAX и BBB, соединяет прямую линию 1.

В этом случае, чтобы найти расположение центра конечного поворота плоскости трапеции, необходимо продолжить прямые линии AB и Λ,/^.Их точка пересечения будет центром вращения объекта. Однако если (рис.6.2, c), средняя точка [) и/::соединяет точку A с точкой B и точкой Bb, то множество перпендикуляров к прямой является параллельным, то центра конечного вращения нет. II определение и исследование состояния вращения печи также recommended. In л 1)

Выберите 2 точки в исходном положении плоской формы. 2)найти положение той же точки после окончательного перемещения фигуры. 3) соедините начальное и конечное положения каждой из 2 точек на рисунке прямой линией. 4) в центре этих отрезков восстановите перпендикуляр к этим прямым линиям и пересечение этих перпендикуляров, найдите нужный центр конечного поворота вида в плане. Задача 6.3.Колесо вращается на прямом рельсе без скольжения. Если колесо перемещается так, что точка соприкосновения колеса и рельса является самой дальней точкой от рельса, найдите положение центра последнего оборота (рисунок а).

Смотрите также:

Предмет теоретическая механика

Сложение ускорений	Скорости точек плоской фигуры
Кинематика колебаний	Подвижная и неподвижная центроиды