Оглавление:


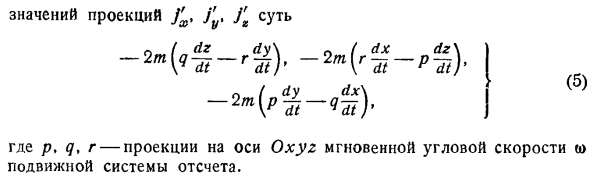

Уравнения относительного движения точки
- Уравнение Лагранжа, как мы видели ранее, позволяет нам найти относительное движение точек на системах, которые выполняют известные нам движения пункты 259, 263, 282. Кроме того, мы можем видеть, что то же самое уравнение применяется к относительному движению голономной системы. Поэтому нет необходимости строить специальную теорию относительного движения. Тем не менее, мы исследуем непосредственно, принимая во внимание важность вопроса. Задачи таковы: под действием определенной силы она дает неизменную систему S, которая совершает определенные движения, и материальную точку m. It необходимо найти движение этой точки относительно системы S, которая называется движущейся точкой отсчета frame.
Они будут алгебраическими относительно координат тел и их первых производных. Это будут семь общих уравнений движения, применимых к произвольной механической системе. Людмила Фирмаль
To определить движение системы отсчета S, достаточно определить движение 3 осей Ox, Oy, Oz, которые всегда связаны с этой системой, как видно из кинематики раздел 45.Точка m, в каждый момент времени абсолютная скорость VA, имеет относительную скорость VR относительно системы отсчета s, а подвижная скорость ve. Существует векторная зависимость между этими 3 скоростями ва = ВР + Ви. Существует аналогичная формула ускорения, включающая дополнительные условия. O это абсолютное ускорение, относительное ускорение младший, Йе портативный ускорение, и J это вектор называется добавочное ускорение.
- Векторы равны а = = Младший + Йе + З 1 Вспоминая эти результаты, мы переходим к интересующему нас вопросу. Поскольку результирующая сила F силы, действующей на точку m, равна абсолютному ускорению Ja, умноженному на массу точки m, 2 3 На основе равенства 1 возникает новое векторное равенство: откуда Это векторное уравнение преобразуется в 3 алгебраических уравнения, которые получаются при проектировании рассматриваемого вектора на движущемся axis. In таким образом, мы получаем уравнение так называемого относительного движения. Проекция Jr на движущуюся ось Oxyz равна X, Y и Z.
Проекция силы F через Je x, Je p A 2, является проекцией переносного ускорения, а проекция дополнительного ускорения через y , y .Тогда есть 3 уравнения. м Р2. У е г г d2z З.. 2 = 2 м а = мг. 4 Проекции ускорения je и y известны. Это происходит потому, что движение системы отсчета S, или одинаково переносимой, известно. Интегрируя дифференциальное уравнение 4, получаем уравнения относительного движения функций t, x, y и r, то есть в конечной форме. Векторам mje и mJ , проекции которых включены в уравнение 4, даны следующие специальные названия: система S равномерное вращение вокруг неподвижной оси.
Из уравнения видно, что выражение суммы элементарных работ заданных сил симметрично относительно динамы. Можно, наконец, получить еще один интеграл при помощи теоремы кинетической энергии. Людмила Фирмаль
Противоположная центробежная сила, равная произведению массы и дополнительного ускорения, вектор МДж, называется кориолисовой инерционной силой. Мы приходим к следующему выводу: относительное движение точек относительно движущейся оси oxyz будет таким же, как если бы эти оси не двигались, добавляя 2 мнимые силы к силе, действующей на движущиеся точки. Еще 1 инерция Кориолиса.
Смотрите также:
Теоретическая механика — задачи с решением и примерами
| Обруч | Кинетическая энергия в относительном движении |
| Свободное твердое тело. Упражнения | Относительное движение по отношению к осям, совершающим поступательное движение |
Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.

