Уравнения не содержащие 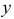
Уравнение вида 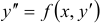 не содержит явным образом искомой функции
не содержит явным образом искомой функции 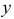 . Порядок такого уравнения может быть понижен с помощью подстановки
. Порядок такого уравнения может быть понижен с помощью подстановки 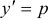 .
.
Пример:
Решить уравнения 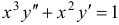 .
.
Решение:
Положим 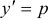 , тогда
, тогда 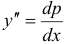 , и мы получаем дифференциальное уравнение первого порядка относительно вспомогательной функции
, и мы получаем дифференциальное уравнение первого порядка относительно вспомогательной функции 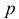 :
: 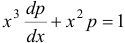 . Это уравнение является линейным. Найдем его общее решение, используя метод вариации произвольной постоянной.
. Это уравнение является линейным. Найдем его общее решение, используя метод вариации произвольной постоянной. 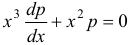 ,
,
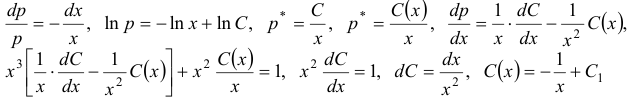
Итак, 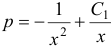 , т.е.
, т.е. 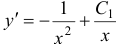 . Следовательно,
. Следовательно,
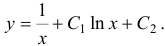
Замечание. Аналогичным способом можно проинтегрировать уравнение 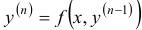 , полагая
, полагая 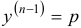 .
.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Уравнение Бернулли |
| Уравнения вида y(n) = f(x) |
| Уравнения, не содержащие x |
| Линейные однородные уравнения с постоянными коэффициентами |

