Оглавление:





Уравнения макроскопических балансов для изотермических систем. Задачи
- В этой главе мы формулируем уравнения макроскопического баланса массы, импульса и механической энергии и показываем примеры применения этих уравнений к решению инженерных задач. Проблемы с гидромеханикой. Задачи 7-1. Несжимаемая жидкость течет в кольцевом канале. Вода перекачивается через насос со скоростью 908 л-мин-1, через соосную кольцевую трубу с уклоном 6.19 м в длину. Внутренний и внешний диаметры труб составляют 7,6 см и 17,8 см соответственно. Разница между верхним и нижним уровнями трубы составляет 1,52 м, а температура воды-15,5°С. найти мощность, необходимую для перекачки water. To решите эту задачу, используя понятие среднего гидравлического радиуса.
Предположим, что давление воды в насосе и давление на выходе из трубы одинаковы. 7-2.Рубка древесины chips. In при производстве бумажной массы целлюлозные волокна, содержащиеся в древесной стружке, освобождаются от связующего лигнина путем нагрева стружки в щелочном растворе под давлением. Раствор помещают в большой цилиндрический резервуар, называемый автоклавом. В конце периода»варки» осадок, состоящий из размягченной древесной щепы, выпускается через узкое отверстие в нижней части автоклава. В дренаж помещают плотно закрепленную пластину path. As в результате воздействия потока в этой пластине происходит интенсивное разрушение стружки и высвобождение целлюлозных волокон.
Проведите анализ размерностей для потока и теплообмена масла через трубу или канал, предположив, что все параметры, за исключением вязкости, могут рассматриватсья как постоянные. Людмила Фирмаль
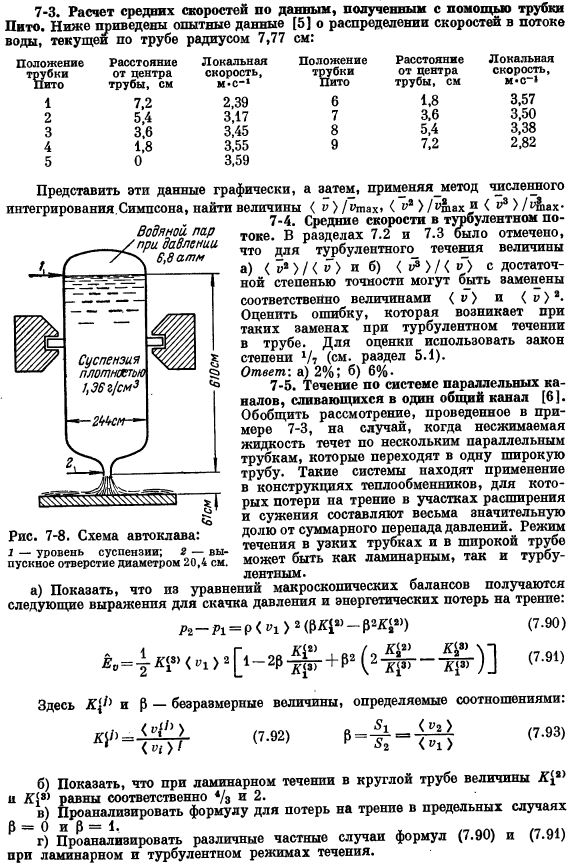
Рассчитайте скорость слива и силу, с которой жидкость воздействует на плиту при выгрузке осадка из автоклава. Исходные данные для задачи показаны на рисунке. 7-8.Влияние трения и кинетической энергии жидкости в автоклаве незначительно. Ответ «да». 1275 кг-с » 1; 4,845-109 Дин. 7-3.Рассчитайте среднюю скорость движения по данным, полученным с помощью трубки трубка Пито. Ниже приведены экспериментальные данные по распределению скорости потока воды по трубе с радиусом 7,77 см[5].
Расположение расстояние местное Трубка от центральной скорости Трубка Пито, см М-1 1 7.2 2.39 2 5.4 3.17 3 3.6 3.45 4 1.8 3.55 5 0 3.59 Расположение расстояние местное Трубка Пито от центра трубы, см скорость, м «с» » 6 1.8 3.57 7 3.6 3.50 8 5.4 3.38 9 7.2 2.82 Число. __ В8> / Лах- 7-4.Средняя скорость движения turbulence. In в разделах 7.2 и 7.3 мы отметили, что для турбулентных течений величины a) p *> / p> *и 6)»I> / p»могут быть заменены с достаточной точностью значениями p>и p> a соответственно. Оцените погрешности, возникающие при таком обмене в турбулентном потоке в трубе. Используйте следующие права в том, чтобы оценить? (См. Раздел 5.1).Ответ: А) 2%. Б) 6%. 7-5.
Поток вдоль системы параллельных каналов, сливающихся в 1 общий канал (6) для обобщения соображений примера 7-3, когда несжимаемая жидкость течет по нескольким параллельным трубам, проходящим через 1 широкую трубу. Теплообменники, в которых потери на трение в зоне расширения и сжатия занимают очень большую долю от общего перепада давления. Течение узкой трубы и широкой трубы является либо ламинарным, либо турбулентным. способ применения 1 после отображения этих данных графически._ _ Интегрированный Симпсон, количество V) / Pmax (y2) / ^ max найти Водяной пар _____ /С давлением 6.6 АТМ 1,36 г суспензии{см3 Рисунок 7-8.Автоклав схема: 1-уровень остановки.
Розетка диаметром 20,4 см а)из уравнений макроскопического баланса показано, что для скачков давления и потерь энергии на трение получены следующие уравнения: Р2_Р1=р> > 2-Р2Я?>) (7-90) Кей? П к )] (7.91) Здесь с ярлом P-безразмерная величина, определяемая соотношением: 1>(7.92) p = A =(7 ′ 93) П / > / » 2 $ Р1> Б) для ламинарного течения круглой трубы значение и указывают, что оно равно 4 / С и 2 соответственно. в)проанализировать формулу потерь на трение в крайних случаях г) проанализировать различные частные случаи формулы (7.90) и (7.91) в условиях ламинарного и турбулентного течения.
Расчет средней скорости ламинарного течения неотонической жидкости в кольцевой трубе, а) поиск значений с. 2 (7.94) 7 ^(3)_ x Р3> — р> с (7.95)) Определяется при рассмотрении предыдущего вопроса. Для неньютоновских жидкостей они движутся по длинной круговой трубе в ламинарной области в соответствии с законом вязкой мощности [формула (1.8)]. Отметим возможность использования значений K1>Для описания соотношения средних скоростей, содержащихся в уравнениях макроскопического баланса (7.5) и (7.7) в виде произведения импульса потока и кинетической энергии на соответствующий поправочный коэффициент.
Выполните аналогичный расчет для жидкости, характеризуемой моделью Бингема. Ответ: а)=(Х4-1)/(2×4-1); b)^ 8)= 3(3n4-1) 2 /(2n-b1) (5n4-3). 7-7.Фрикционные потери неньютоновской жидкости. Жидкость, описанная в законе вязкой мощности (1.8), течет ламинарным потоком через круглую трубу радиуса B и длины B. In задача 2-6, мы нашли распределение скорости такого потока.
Указать, что профиль скорости может быть выражен следующим образом: / 3n4-1 \ [/\р(п + 1)/ н- | ] 7-98> b) используйте формулу на стр. 205, чтобы явно записать подынтегральное выражение уравнения потерь на трение (7.21).Вычислите Интеграл и докажите связь 2нм п> п + 1, 1 * ’=- — — — — — I ’ −1 (3 + tg) 7-«) в)вы можете видеть, что применение формулы (7.28) дает тот же результат. Расчет коэффициента ламинарного трения неньютоновской жидкости в трубе проводился в задаче 6-7. 7-8.Изменение режима подачи газа из газгольдера.
- Природный газ течет по газопроводу в Газгольдер с постоянной массовой скоростью> 1. Подача газа из газгольдера и 2 будет меняться в течение суток практически по закону и что?2 =а, 4 — Б, потому что(с (7.100) Здесь Юг — это безразмерное время, измеряемое с момента, соответствующего максимальному расходу газа (например, с 6 часов утра).Газ)и? рРве3ерв7аЬраТ2, » ное » минимум и среднее значение b) значения A и B используются для представления скорости поступления газа в Газгольдер. В) использовать начальное условие m = u0 с 2 = 0 для интегрирования уравнения нестационарного баланса массы газа в Газгольдере. Найти массу M как функцию времени.
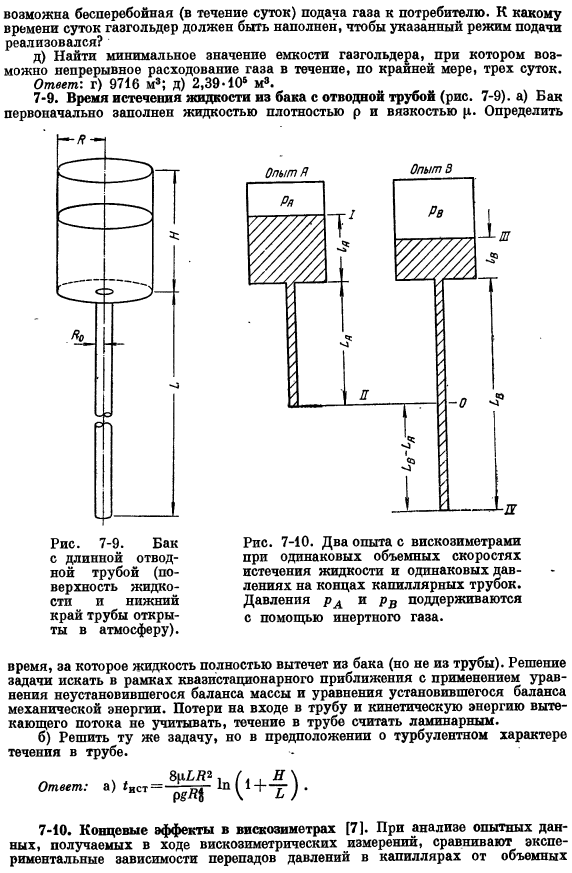
После установки г-см » 8, определяют минимальное абсолютное значение емкости газгольдера без перерыва (сутки) подачи газа потребителю. В какое время должен быть заполнен Газгольдер для реализации указанного режима потока? д) найти минимальную емкость газгольдера, которая может потреблять газ непрерывно в течение не менее 3 суток. Ответ’, г)9716 м3; д) 2,39 * 105 м3. 7-9.Время истечения жидкости из резервуара с дренажной трубой(рис. 7-9). а) резервуар сначала заполняется жидкостью плотности р и вязкости р. идентифицировать — Я.- −3 с => 2 ^ 3 секунды- Рис. 7-10.
В текучем состоянии падение давления должно быть равным весу слоя, поэтому начало состояния текучести может быть вычислено следующим образом: Плотность частицы определяется как плотность слоя в уплотненном состоянии, предшествующем состоянию текучести. Людмила Фирмаль
Эксперименты с использованием вискозиметра с одинаковым давлением при одинаковом объемном расходе и концах капилляров. Давление PA и PB с инертным газом. 7-9.Резервуары с длинной выпускной трубой(поверхность жидкости и нижний конец трубы открыты для атмосферы); Время, пока жидкость полностью не выйдет из бака (но не из трубы).Решения этой задачи найдены в рамках квазистационарных приближений с использованием уравнений нестационарного баланса масс и уравнений стационарной механической энергии balance. Do не учитываются потери на входе в трубу и кинетическая энергия стока. Поток в трубе следует рассматривать как ламинарный поток.
Решает ту же задачу, но предполагает турбулентный характер течения в трубе. Ответ: один) 7-10.Конечный эффект вискозиметра[7].При анализе экспериментальных данных, полученных при измерениях вязкости, проведено сравнение экспериментальной зависимости перепада давления в капилляре от объемной скорости жидкости с теоретическим уравнением перепада давления в зависимости от расхода. Теоретическое выражение основано на предположении о полностью развитой характеристике течения пространства между 2 плоскостями, в котором измеряется давление.
В случае вискозиметра, показанного на рисунке от 7 до 10, значение давления проверяется в выходном сечении трубки (плоскость II) и выше уровня жидкости в баке(плоскость G).Однако в первой секции трубы профиль скорости не полностью разработан. По этой причине теоретическая зависимость между перепадом давления и объемным потоком (например, закон Ньютона Хаагена-дазааля) не применима к начальному сечению. Однако существует способ экспериментально исключить влияние первого раздела, тем самым обрабатывая экспериментальные данные с использованием закона Хаагена-даже.
Этот метод основан на том, что он выполняет измерения в 2 трубках разной длины (bA и bb).Длина короткой трубки*должна быть достаточно большой, чтобы профиль скорости на ее конце мог быть полностью established. In в этом случае конец длинной трубки (как видно из рисунка 7-10, ее длина равна L) будет явно представлять собой область полностью развитого потока. Если разность давлений P0-P4 в этой области определена, то дальнейший анализ может быть выполнен с использованием уравнения Хагена-Пуазейля (2.46). Запишите уравнения равновесия для механической энергии систем 1-ЩIII-IV и 0-IV. Если объемный расход всех Вискозиметров одинаков, то соотношение ПП-П _ _ ПВ-Ра.
Где Po = Po 4-P#2o, а величина Po-P характеризует эффективную разность давлений на участке длины 1’b-bA * Объясняет, как анализировать результаты измерений, используя формулу (7.101).Применяется ли эта формула также к трубам некруглого сечения? 7-11.Сила, действующая на стенку кольцевого канала, коррелирует с фрикционными потерями этого канала. Проверить применимость уравнения (7.28) для ламинарного течения несжимаемой ньютоновской жидкости в длинном кольце channel. To проверьте, используйте профиль скорости, полученный в разделе 2.4.Длина канала обозначается через b, внутренний и внешний радиусы, xH и H соответственно.
Эффект ускорения обусловлен нестационарным оттоком жидкости из пласта. Цилиндрический резервуар высотой H и радиусом I открыт сверху, сначала заполненный жидкостью до края. В момент I = 0 жидкость начинает вытекать из бака через узкое отверстие Яо, радиус которого выполнен на дне бака. а) в первом приближении используйте формулу Торичелли расхода как функцию мгновенной высоты жидкости для оценки времени истечения жидкости из резервуара- б)определить срок годности с использованием уравнений переходного баланса массы и механической энергии. Функция параметра n =(Я/Яо) представляет результат в виде произведения расчетного времени в пункте»а».
Оценить значение поправочного коэффициента, полученного в разделе»в». Ответ: b) / и » = 2(Л / Л0) 2 /я727р(Л)、 Один Где: Φ^)= 1 /(T ^ 2) TLG 7-13.Распределение скоростей в ответвлении трубопровода. Жидкость течет по трубе, которая заблокирована с одной стороны. Параллельные сопла отходят от трубы, диаметр которой такой же, но отличается от диаметра основной трубы.
Смотрите также:

