Оглавление:










Уравнения Лагранжа
- Из (30) получите второй тип уравнения Лагранжа или просто уравнение Лагранжа. Первый тип уравнения Лагранжа — уравнение с неопределенным множителем Лагранжа — это гл. 8 очков зарабатываются в одной точке. 1. Вы также можете получить лагранжево уравнение первого рода системы. Тождество Лагранжа. Чтобы получить уравнение Лагранжа, вам нужно три идентификатора. Одна из них — известная формула для дифференцирования скалярного произведения любых двух векторов a и 5. или дд дф Если вектор скорости vk = rk и B является вектором 3r.
Согласно этой идентичности (3 ” Другая идентичность (тождество Лагранжа) выражается как drk / dqi = dfk / dql (32) Здесь точка над количеством означает производную по времени. Величина q — AqJAt называется обобщенной скоростью. Идентичность (32) указывает, что вы можете установить «точки» (производную по времени) или «сокращения» одновременно для числителя и знаменателя. Эффективность (32) доказывается путем расчета содержащихся в нем величин и сравнения их. На самом деле, общий случай По мере движения системы обобщенные координаты также являются функцией времени. Дифференцируя рк по времени как его сложной функции, , Дгк д дгк. DGK + 77-J], 4 ″ + p.
Другими словами, это отношение будет одним и тем же, каковы бы ни были физические условия возникновения ускорений, будь то наэлектризованность, взаимное давление, ньютоновское действие и т. Людмила Фирмаль
Частная производная dgk / dh (и drk / dl не может зависеть от обобщенной скорости qt. Поэтому, если вы дифференцируете с фиксированным числом (33) обеих частей определенным образом по отношению к cc, только коэффициент этой переменной Все остальные члены производной дают ноль, которые не зависят от этого фиксированного числа qt. dfk / dqi = drkldql. Тождество (32) доказано. Другим лагранжевым тождеством является перестановка порядка дифференцирования по времени и обобщенным координатам вектора rk. s (S) — & (34).
Чтобы доказать это тождество, используйте (33) для вычисления drk / dqt, учитывая, что обобщенная скорость не зависит от обобщенных координат. получить dggk d2fk дк, 8т ‘ (35) Drkldqt, с другой стороны, является сложной функцией времени и зависит не только от явных, но и от обобщенных координат. Из-за правил дифференциации сложных функций, д Здра 32фк. dggk. A2g,. a2rt ди \ S9i) ^ 4i ^ 4i ^ 1dHhdH) ^ H ^ H, ^ ‘dtdqi’ (36) Вы можете изменить порядок частных производных смешанных производных. С учетом этого (35) и (36) совпадают. Таким образом, тождество второго Лагранжа доказано. Вывод лагранжевых уравнений.
Чтобы получить обобщенное лагранжево уравнение инерционной силы из (30), нам нужно доказать справедливость где -Кинетическая энергия системы, как она движется относительно инерциальной системы отсчета. Для доказательства (37) используем определение по силе инерции Φ4 = -mkak = -mkkk, £>! Вычислить Ф). У нас есть (38) Преобразовать выражение 0t S4i По тождеству (31) (-J. D (d ^ \ Tk dqt dt y * dqj T * dt \ dqtJ Применить тождество Лагранжа. 0ft _ 0r4 _ 0i>, d I Bfk | _ 0g «_ 00» dqt dqt dq, d / \ 0 cc Трение вала винта игнорируется. Движение начинается с состояния покоя. L •. К я Решения. Мобильная система имеет две степени свободы. Обобщенные координаты системы берут 5 перемещений произведения по «плоскости и углу».
Наклонная нагрузка Кинетическая энергия системы Инерция диска Где vc — центральная скорость Промах! G — радиус диска относительно оси, проходящей через центр диска Блок В вращается вокруг неподвижного Где <р! Является ли угловая скорость блока. Jc g = ось вращения; g} — радиус блока. Груз D) Движение доступа Перпендикулярно плоскости Относительный момент инерции Энергетическая энергия Предположим, что неразвернутая резьба блока ориентирована в положительной плоскости, поскольку она связана со скоростью 1 точка. Так что в начале загрузки Ускорение нагрузки вниз. Все вязать Скорость число | s |. Следовательно, такая скорость и точка диска М.
- Возьмите его с помощью шеста и определите скорость точки по формуле, которая соединяет скорость двух точек тела с плоскостью Где 1> см = L / C | φ |. Когда диск вращается против часовой стрелки, скорость «см» будет вертикально вниз, а когда груз будет перемещен, он будет вертикально вверх I) вниз е) 2 Выразите кинетическую энергию системы с обобщенной скоростью 2 2 2e 2 Вычислить производную, которая попадает в левую часть уравнения Лангранжа: d dT sp ‘ dtdif 2g f g При расчете обобщенной силы необходимо учитывать гравитационные силы P и P2 и силу трения F на наклонной поверхности.
Нет необходимости учитывать идеальное сочетание реакций (винты, блочные оси, плавные пандусы). Выберите правильное направление силы трения F Важно Сила трения F всегда направлена на скорость s перемещения груза D, которая не всегда известна заранее. Предположим, что движение груза происходит вниз, но на наклонной поверхности. Тогда сила трения в противоположном направлении. Решите проблему в этом предположении. Если вы используете знак плюс, чтобы получить s (в данном случае s, потому что он начинается из состояния покоя), принятое предположение верно.
Если наблюдатель был вначале неподвижным, а затем пожелал двигаться, то его центр тяжести движется как материальная точка, вначале неподвижная и находящаяся под действием вертикальной силы. Людмила Фирмаль
Если ускорение z (и, следовательно, скорость z) отрицательно, было обнаружено, что ожидаемое направление силы трения направлено вдоль движения нагрузки, поэтому направление силы должно быть обращено вспять, и проблема будет решена снова. Это неправильно Когда j ’= 0, нагрузка не может быть перемещена из стационарного состояния. Как только предполагаемое направление силы трения на наклонной поверхности установлено, вычисляется обобщенная сила Q. В то же время он информирует систему о возможных перемещениях, допускаемых соединением, и под этим углом сообщает движениям, что груз может упасть на рампу. 6 секунд.
Если φ = const, смещение точки C диска такое же, как смещение точки M, поэтому F = Fmtl = / N сила Pt применяется к неподвижной точке и возможна потому, что возможное движение неподвижной точки равно нулю Вся основная работа по переезду равна нулю. Вертикальная сила реакции на наклонной поверхности определяется из баланса силы нагрузки D в направлении, перпендикулярном наклонной поверхности. У нас есть Имея это в виду b, = P2 (sin <x-f cosa) —P. При расчете обобщенной силы 1 смещение, где изменяется величина 8 <p, и обобщенные координаты положительный В этом случае точка диска М является оростом, 8cc = r8 <p и 8cc положительный 8 <p направление R.
Другие рабочие места перемещения равны нулю, потому что их очки Go. Вот так Одновременные уравнения Уравнение Лагранжа, получить — / cosa) —P; Выразите от φ до s из последнего уравнения. ψ = — (+ + 3). Подстановка этого значения в первое выражение приводит к + .P2j = P2 (sina-7cosa) — ^ Знак плюс для s (в данном случае для s) указывает на то, что, как и ожидалось, движение I) фактически направлено вниз вдоль склона.
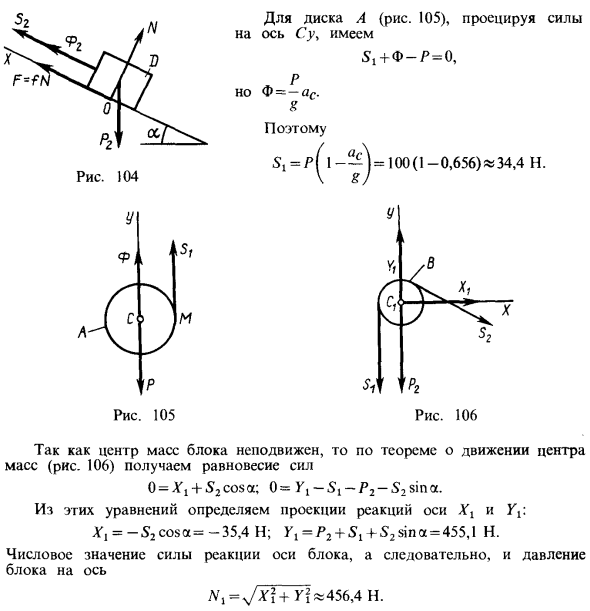
Ускорение в точке C можно получить путем дифференцирования по времени уравнения скорости Vc = s-rf. Это действует в любое время. У нас есть Вот так. ac = ‘»c = i-r <P = j- ^ (g + i) =» j «= -0,656x = -6,43 м / с2. Знак минус для переменного тока указывает, что ускорение переменного тока направлено вниз. Это потому, что направление вверх является положительным направлением. Чтобы определить натяжение нити, принцип Дарренвале применяется к нагрузке и диску. Для нагрузки D (рис. 104), которая проецирует силу на ось Ox, получается S2 + <K2-P2sina + / W = 0. но так Н.
Смотрите также:
Задачи по теоретической механике
| Условия равновесия системы | Тождества Лагранжа |
| Общее уравнение динамики | Вывод уравнений Лагранжа |

