Уравнения Громеки при действии массовых сил, имеющих потенциал

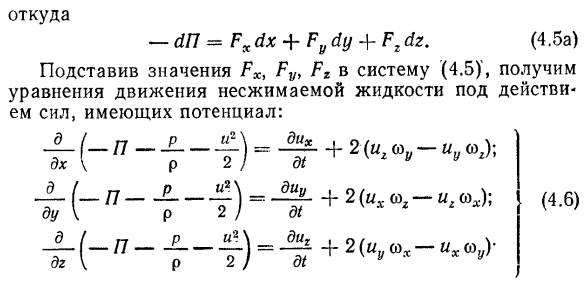
Уравнения Громеки при действии массовых сил, имеющих потенциал

Уравнения Громеки при действии массовых сил, имеющих потенциал. Если массовые силы, действующие на жидкость, имеют потенциал, то проекция Px, Py> Pr плотности распределения массовых сил выражается в виде частной производной от потенциальной функции P. г ДП ДП ДП д ДП ■р «Так… Откуда? -гг-Пх-ых + ру ю + Ю. г. Пр. (4,5 а).

Уравнения Громеки бывают в некоторых случаях более удобными, чем обычная запись уравнений Эйлера. Людмила Фирмаль

• Подставляя значения Px, Py и Pr для системы (4.5)’, получаем уравнения движения несжимаемых жидкостей под действием потенциальных сил. −1 ДХ 1(-р-р п \ А2 2 / второй ^ Я * я 5(-П-П У2 \ Диу дю \ Р 2 / Д1 ’/7-р и 2) 1 _ di * dg’P 2) ’ d1 + 2(СГ&г-Йи Юг); + 2(ihag-и ко*); + 2(ю и х-их (ЮУ (4.6)）

В частности, их удобно использовать при получении интеграла Бернулли и интеграла Коши — Лагранжа. Людмила Фирмаль

Смотрите также:

Задачи по гидравлике

Возможно эти страницы вам будут полезны:

1. Дифференциальные уравнения движения невязкой жидкости (уравнение Эйлера).
2. Уравнения движения невязкой жидкости в форме Громеки.
3. Уравнение Бернулли для установившегося движения невязкой несжимаемой жидкости при действии массовых сил, имеющих потенциал.
4. Уравнение Бернулли для частных случаев.