Уравнения движения вязкой жидкости (уравнения Навье—Стокса)

Уравнения движения вязкой жидкости (уравнения Навье—Стокса)

Уравнения движения вязкой жидкости (уравнения Навье—Стокса). Состояние движения реальной (вязкой) жидкости удобно классифицировать по соотношению влияния вязких и динамических(инерционных) сил. Движение вязкой жидкости описывается уравнением Навье-Стокса, которое получено на основе уравнений движения Эйлера(4.15) с учетом действия вязких сил. На основе формулы (5 4), выражающей закон трения, рассмотрим неточный (иллюстративный) вывод уравнений движения вязких жидкостей.

Что касается уравнения непрерывности, то, как явствует из самого его вывода, оно относится в равной мере к движению всякой жидкости, в том числе и вязкой. Людмила Фирмаль

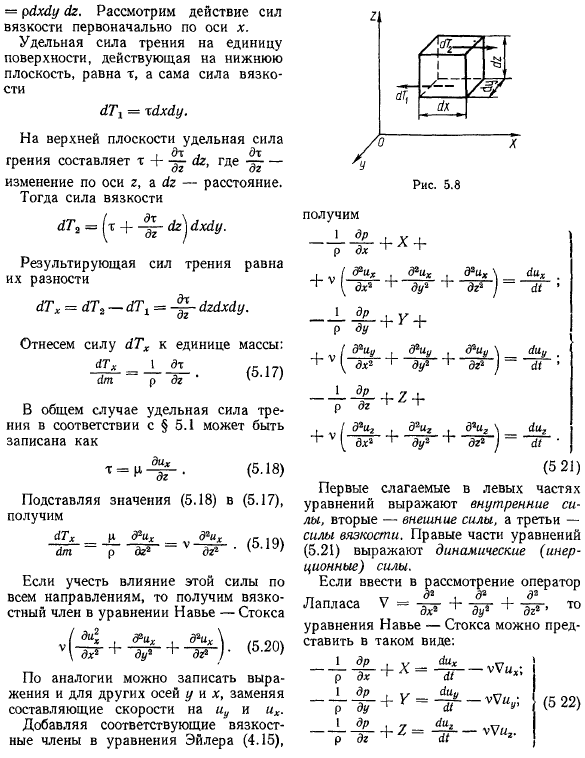
• В потоке жидкости выбирают бесконечно малые объемы жидкости в виде параллелепипеда (рис.5.8) с массой =Am. 82. = rihyu мкг. Сначала рассмотрим действие вязкой силы вдоль оси X. Удельная сила трения на единицу поверхности, действующая на нижнюю плоскость, равна t, а сама вязкая сила равна 6TX =huhuhu. На верхней поверхности удельная сила трения равна m + ^ Lr. Здесь. изменения вдоль оси Z. ДГ-это расстояние.

Тогда вязкая сила ст2 = ^ Р + ДГ ^ dxdu. Результирующая сила трения равна разности между ними для DTX = ст2-ст1 = ygdhyu. Свяжите силу tx с единицей массы. yth _ _1_ ДХ ыть-Р ДГ ’ Мы получаем (5.17） 1. П. С. 1-+ * + + В d2ih д *им+ d2ih \ 1 4ih dx2 1 du2 dg2)1 d1 1. Р%-+ * + Дху dx2 1 1 ду2. d2iu’dg2 второй 1. П% г + 2 + + V / dCh2 d2ig dx2 1 dv2•+ d2u, ’ dg2 \ У1. В общем случае удельная сила трения согласно § 5.1 равна、 х = р Ров. дециграмм. (5.18） При присвоении значения (5.18) (5.17)、 4TX d2ih d2ih ыть Р почтовый индекс dg2 почтовый индекс dg2 (5.19).

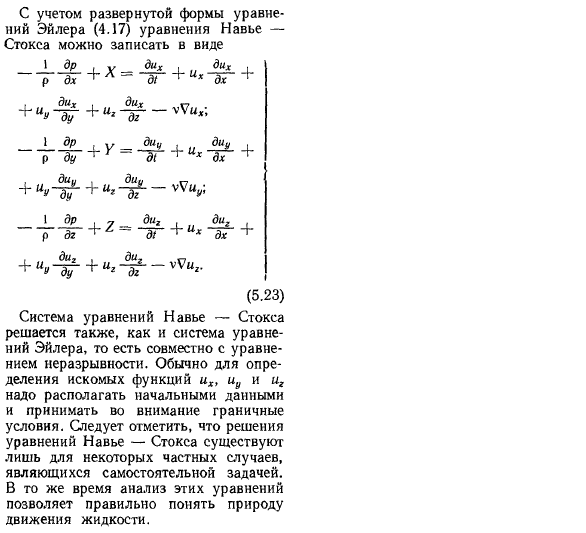
• Если учесть влияние этой силы во всех направлениях, то получим вязкий член в уравнении Навье-Стокса. ’* <+ dx2 ^ d2ih dhh DN2 по■+ почтовый индекс dg2 (5.20） (5 21） Первый член в левой части уравнения представляет собой внутреннюю силу, второй-внешнюю силу, а третий-вязкую силу. Правая часть уравнения (5.21) представляет собой динамическую (инерционную) силу. С введением оператора d2 d2 d2 Лаплас V = = ^ g + ^ g + 70 Уравнение Навье-Стокса может быть выражено как.

Аналогично можно описать формулы других осей скорости, заменив компоненты скорости на yiu. Добавьте соответствующие вязкие члены в уравнения Эйлера(4.15）、 д-р __ <&х ДХ » г» ±.Б + г = С. С. ±%+2 = Р, Д, 1. тн1. да. <И ИММУНОГЛОБУЛИН. ■Причина\ Обхаживать. 』 (5 22） 83. Рассматривая расширенную форму уравнений Эйлера(4.17), уравнения Навье-Стокса можно записать в виде: −1. Р д-р. ДХ в час » Х =д / 4-они■Дих ДХ 4. » Праведность у 4 ″ ИГ Ди ^ ДГ ■ chuih、 -_1_ Р д-р. Пришло время… _ | _ У -Диу Д1 4-они ■ Диу ДХ 4. » + Диу в сделать +» *■Диу ДГ вуюу 1. Р д-р. dg 4 ″ = 2-рытье d1 4-их копать.

Поэтому уравнение движения вязкой жидкости можно получить, прибавив к «идеальному» потоку импульса дополнительный член, определяющий необратимый, «вязкий», перенос импульса в жидкости. Людмила Фирмаль

• Система уравнений Навье-Стокса решается так же, как и система уравнений Эйлера, то есть вместе с уравнениями неразрывности. Обычно для определения функций yi и yi по их назначению необходимо получить исходные данные и учесть граничные условия. Следует отметить, что решение уравнения Навье-Стокса существует только в некоторых частных случаях, которые являются независимыми problems. At в то же время анализ этих уравнений позволяет правильно понять характер движения жидкости.

Смотрите также:

Задачи по гидравлике

Возможно эти страницы вам будут полезны:

1. Два режима движения жидкости.
2. Распределение касательных напряжений при равномерном движении.
3. Характеристика ламинарного режима движения жидкости.
4. Характеристика турбулентного режима движения жидкости.