

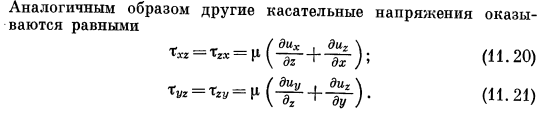

- Давайте еще раз подумаем о рисе. 11. 1 и напишите уравнение из 31 компоненты силы, возникающей при изменении напряжения в пространстве. ЛРХ ех = * г +(mUx4-Лу)&+ Н^ 2 ^(1х(1у-Тхх-» ^ух&&Ухх^У-(11•8. После упрощения это уравнение имеет вид ar1aapr=(-^ + ^ + ^)^^ чт. (11.9) Единственная сила, действующая в направлении оси x, — это уравнение напряжения (I. 9), а формула силы массы (11.5)-результирующая сила. Уравнение (I. 4) входит в уравнение (I.), поскольку члены CMX равны сумме этих сил 4), (I. 5), (11.6)и (I. 9) из е ^ = е? CO8P + ^+^ + ^. 1-10. Формула (I. 10)описана в разделе напряжение.
После упрощения это уравнение имеет вид ar1aapr=(-^ + ^ + ^)^^ чт. (11.9) единственная сила, действующая в направлении оси x, — это уравнение напряжения (I. 9), а формула силы массы (11.5)-результирующая сила. Уравнение (I. 4) входит в уравнение (I.), поскольку члены CMX равны сумме этих сил 4), (I. 5), (11.6)и (I. 9) из е ^ = е? CO8P + ^+^ + ^. (11-10) Формула (I. 10)описана в разделе напряжение.
Читатель помнит, что эти напряжения также можно рассматривать как плотность магнитного потока составляющих импульса. Дик и Х экспрессы результирующая плотность магнитного потока α-составляющей импульса от выбранного объема проходит через 2 плоскости, перпендикулярные оси X. Термин & y общая плотность магнитного потока » — com- компонент импульса от выбранного объема через плоскость, перпендикулярную оси Y. Уравнение (I. 10) последние 3 члена имеют аналогичное значение, а уравнение(9. 18) (массовый расход) и уравнение (10. 8) можно сравнить с аналогичными терминами (поток энергии).
В дополнение к уравнению (11.10) можно создать аналогичное уравнение для направлений осей y и 2.To чтобы было еще проще ссылаться, мы опишем все 3 уравнения. е — ^ = е+ ^ + ^-+ ^-; (второй) е ^ = ЕС + ^ + ^ + ^ ^ ы. (11.12) е> = е * + ^ + ^ + ^. (I. Тринадцать) Следующим шагом является вывод уравнения, пригодного для расчета перепада давления или распределения скорости. Для этого напряжение связывают со скоростью деформации элемента и вязкостью жидкости. Скорость деформации выражается производной от составляющей скорости движущейся жидкости. Для неньютоновских жидкостей формула I.
- Остается действительной, но скорость напряжения и деформации должна быть изменена в последующем описании, которое обычно связано через вязкость. Зависимость между вязкостью и напряжением 1 Напряжение на растяжение С другой стороны, упругое тело деформируется пропорционально напряжению зако Насос на крючке. Убедитесь, что величина деформации ньютоновской жидкости пропорциональна скорости деформации. (Скорости деформации иногда называют скоростями сдвига.) Как указано в разделе. 7, формула для определения вязкости по скорости сдвига в случае 1-D является、 Они м^ = — (I. Четырнадцать) Рис. 11.4.Деформация, вызванная сдвигом одномерного потока.
Для более сложных деформаций скорость деформации — это скорость изменения угла Рисунок I. 4.Простой В случае одного измерения изменение угла f (Радиан) относительно времени 1 представление продолжается до[79], значение дуги и V (1m Радиус (1 год С?(Р = (Низ / хорошо) хорошо, Нью-Гемпшир хорошо (I. Пятнадцать) Следовательно, скорость деформации б? низ Ф Они-ну (11. Шестнадцать) Это формула (I. 14) после подстановки、 (I. Семнадцать) Рисунок 11.5.Деформация из-за напряжения сдвига.
А — до деформации; Б-после истечения их времени. Здесь, при исследовании деформации элементов уравнения (I. 17). Рисунок 11. На рис. 5 показана деформация, вызванная напряжением, действующим на плоскость, перпендикулярную плоскости xy. Эти напряжения также показаны на рисунке. Как показано на рисунке. 11. 5, B, изменение угла состоит из 2 частей.1 из них является формулой (I.
Как видно из аналогичных аргументов в выводе equal (часть равна (следовательно—、 Другой * Ф _ 1 Диг, 1 Диу \ HX в 1 1 dx) (I. Восемнадцать) Формула этого утверждения(11. 17).、 / Дих Мне.\ г ДХ. 11.
Смотрите также:
| Дифференциальное уравнение энергии | Нормальные напряжения |
| Уравнения в напряжениях | Уравнения Навье — Стокса |
