Оглавление:



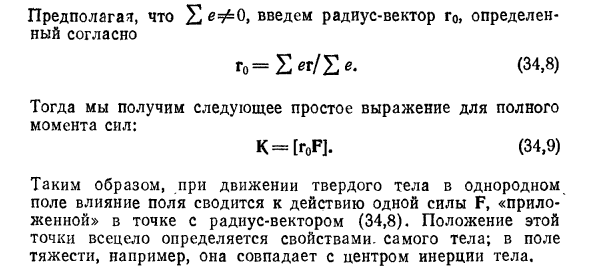

Уравнения движения твердого тела
- Уравнение движения твердого тела. Вообще 6 для твердых тел Для степеней свободы общая система уравнений движения должна содержать шесть независимых уравнений. Они могут быть выражены в форме, которая определяет производную по времени двух векторов, импульса и момента тела.
Первое из этих уравнений получается простым суммированием уравнений p = f для каждой частицы, составляющей объект. Где p — импульс частицы, а f — сила, действующая на нее. Полностью ввести импульс тела p = Јp = tsu И общая сила, действующая на него = F, f = F (34,1) Я определил F как сумму всех сил F Для каждой из этих частиц, включая частицы от других частиц в теле, фактически только силы, действующие от внешних источников, вводят F.
потенциальная энергия внешнего твердого тела Людмила Фирмаль
Все силы взаимодействия между частицами тела сводятся друг к другу. Фактически, в отсутствие внешних сил, импульс тела должен быть сохранен, как закрытая система. Должно быть F = 0. Когда U — В случае поля сила F может быть определена путем дифференцирования с координатами центра инерции тела. F = -1- (34-2)
Конечно, с поступательным движением тела 5R, радиус-вектор r каждой точки тела сильно изменяется, поэтому потенциальная энергия изменяется s = Ј5> = wЈf = -6RЈf = -F6R В этом контексте уравнение (34.1) Как уравнение Лагранжа для координат Центр инерции d d_ _ d__ dtdV ~ dk Функция Лагранжа (32.4) — = А V = P- = = F dv c’di di
- Перейдите к выводу второго уравнения движения, которое определяет производную по времени от импульса М. Чтобы упростить вывод, выбор «Фиксированной» (инерционной) системы отсчета останавливает центр инерции тела в данный момент. У нас есть m = | E [g p] = Ј [g] + E [g].
Благодаря выбору системы отсчета V = 0) Значение r в данный момент времени соответствует скорости v = r. Поскольку векторы v и p = mv имеют одинаковое направление, [gr] = 0. Если р заменяется силой F, Наконец-то получаем: ^ = К, (34,3) где K = S> f]. (34,4) Поскольку момент М определяется относительно внутреннего центра, (См. Начало § 33), которая не меняется при переходе от одного инерциального кадра к другому.
полученная здесь с определенным выбором систем отсчета и Людмила Фирмаль
Это видно из уравнения (9.5), где R = 0. Это уравнение движения (34.3), , следовательно, действительная в любой инерциальной системе, благодаря принципу относительности Галилея.
Вектор [rf] называется моментом силы f, поэтому k Сумма всех моментов силы, действующей на тело. Как и полная сила F, только общая внешняя сила должна учитываться в сумме (34,4). Сумма всех моментов силы, действующих внутренне по закону сохранения момента импульса Закрытая система должна исчезнуть.
Момент силы, как и угловой момент, обычно зависит от выбора начала координат, где он определен. В (34.3) и (34.4) момент определяется относительно центра инерции тела. При перемещении источника далеко Вектор y точек тела связан со старым r через r = r ‘+ a. так K = Ј [r f] = Ј [r ‘f] + Ј [af] или K = K ‘+ [aF]. (34,5)
Это особенно верно, когда величина момента силы Когда общая сила F = 0, это зависит от выбора источника ( В этом случае говорят, что к телу приложена некоторая сила). Уравнение (34.3) можно рассматривать как уравнение Ла Grunge c ^ d_ _ dL_ dt dC1 d (p По отношению к «вращающимся координатам». конечно Дифференцирование функции Лагранжа (32.4) по компонентам вектора ft дает: L = D L = Mi.
Изменение потенциальной энергии U при вращении объекта на минимальный угол bsr равно bU = -J2 f5r = -Јf [bsr • g] = -bsrЈ [g f] = -KScp, Откуда k = (3 4 -6) Вот так dL_ _ di to д (р 6 (р Предположим, что векторы F и K перпендикулярны друг другу. В этом случае вы всегда можете найти вектор Поскольку уравнение (34.5) K исчезает, оно становится следующим.
K = [aF]. (34,7) Кроме того, выбор является неоднозначным. Добавление вектора, параллельного F, не меняет уравнения (34.7). Следовательно, условие K ‘= 0 дает только четкую прямую линию, а не четкую точку в движущейся системе координат.
Следовательно, с K 1 F действие всех приложенных к нему сил может быть сведено к одной силе F, действующей вдоль конкретной прямой линии. Это особенно касается однородных силовых полей. Форма силы, действующей на материальную точку, f = eE, где E — постоянный вектор, характеризующий поле, Величина е затем характеризует частицу для данного поля х).
В этом случае F = EЈe, K = [geg-E]. Предполагая φ0, введем радиус-вектор GO = §J. (34,8) Далее, получите следующую простую формулу для общего момента силы: k = [r0F], (34,9) Поэтому, когда тело движется равномерно Для поля эффект поля сводится к действию единой силы F, «приложенной» к точке с радиус-вектором (34,8). Положение этой точки полностью определяется свойствами самого тела. В поле
Смотрите также:
| Тензор инерции в физике | Эйлеровы углы в физике |
| Момент импульса твердого тела | Уравнения Эйлера в физике |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

