Оглавление:
Уравнения движения плоской фигуры. Уравнения движения точки плоской фигуры
Возьмем в плоскости движения фигуры 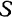 систему координат
систему координат 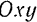 , неподвижную по отношению к этой плоскости. Выберем на фигуре
, неподвижную по отношению к этой плоскости. Выберем на фигуре 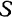 какую-либо точку
какую-либо точку 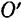 и примем ее за начало другой системы координат
и примем ее за начало другой системы координат 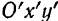 , неизменно связанной с движущейся фигурой (рис. 143).
, неизменно связанной с движущейся фигурой (рис. 143).
Положение подвижной системы координат 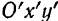 , а следовательно, и самой фигуры
, а следовательно, и самой фигуры 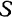 в ее плоскости, определяется положением точки
в ее плоскости, определяется положением точки 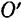 и углом
и углом 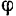 поворота фигуры (т. е. углом между положительными направлениями осей
поворота фигуры (т. е. углом между положительными направлениями осей 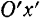 и
и 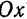 ).
).
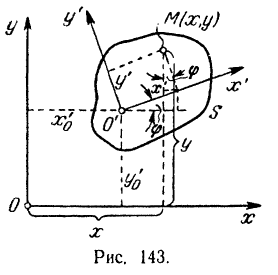
Произвольная точка 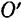 , неразрывно связанная с движущейся фигурой и выбираемая для определения положения фигуры, называется полюсом.
, неразрывно связанная с движущейся фигурой и выбираемая для определения положения фигуры, называется полюсом.
При движении фигуры 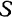 в ее плоскости координаты полюса (в нашем случае точки
в ее плоскости координаты полюса (в нашем случае точки 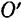 ) и угол
) и угол 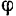 изменяются с течением времени и являются однозначными и непрерывными функциями времени:
изменяются с течением времени и являются однозначными и непрерывными функциями времени:
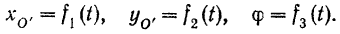
Если эти функции известны, то для каждого момента времени можно найти соответствующие ему значения 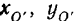 и
и 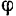 и следовательно, определить положение движущейся фигуры
и следовательно, определить положение движущейся фигуры 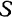 в ее плоскости.
в ее плоскости.
Таким образом, уравнения (98) являются уравнениями движения плоской фигуры 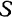 или, что то же, уравнениями плоского движения тела.
или, что то же, уравнениями плоского движения тела.
Если движение фигуры 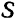 задано уравнениями (98), то нетрудно найти и уравнения движения любой ее точки
задано уравнениями (98), то нетрудно найти и уравнения движения любой ее точки 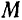 .
.
Как известно из аналитической геометрии (формулы преобразования координат при повороте координатных осей и переносе их начала), координаты 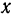 и
и 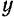 точки
точки 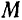 относительно «неподвижной» системы координат
относительно «неподвижной» системы координат 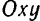 будут выражаться следующими зависимостями:
будут выражаться следующими зависимостями:
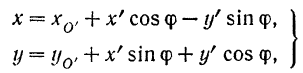
где 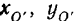 — координаты полюса
— координаты полюса 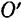 (произвольной точки фигуры),
(произвольной точки фигуры), 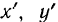 — координаты точки
— координаты точки 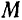 относительно подвижной системы координат
относительно подвижной системы координат 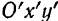 неизменно связанной с данной фигурой;
неизменно связанной с данной фигурой; 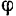 — угол поворота фигуры.
— угол поворота фигуры.
Уравнения (99) являются уравнениями движения произвольной точки 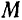 фигуры в ее плоскости.
фигуры в ее плоскости.
Эти уравнения позволяют аналитически определить траекторию, скорость и ускорение любой точки плоской фигуры.
Пример задачи:
Линейка 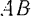 эллипсографа (рис. 144) приводится в движение кривошипом
эллипсографа (рис. 144) приводится в движение кривошипом 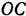 , вращающимся с постоянной угловой скоростью
, вращающимся с постоянной угловой скоростью 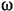 . Составить уравнения движения линейки и ее точки
. Составить уравнения движения линейки и ее точки 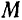 . Найти также траекторию этой точки.
. Найти также траекторию этой точки.
Дано:
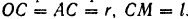
Решение:
Возьмем за начало неподвижной системы координат центр 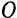 вращения кривошипа. Ось
вращения кривошипа. Ось 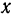 направим горизонтально вправо, ось
направим горизонтально вправо, ось 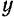 — вертикально вверх.
— вертикально вверх.
За начало подвижной системы координат примем точку  . Ось
. Ось 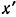 направим вдоль линейки вправо, ось
направим вдоль линейки вправо, ось 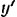 — вверх.
— вверх.
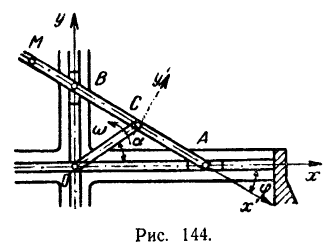
Как видно из рис. 144, координатами полюса  будут:
будут:
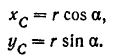
Угол поворота равномерно вращающегося кривошипа 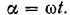 Из рис. 144 нетрудно видеть, что направление поворота линейки эллипсографа относительно полюса
Из рис. 144 нетрудно видеть, что направление поворота линейки эллипсографа относительно полюса  противоположно направлению вращения кривошипа, следовательно, соответствующий углу а поворота кривошипа угол
противоположно направлению вращения кривошипа, следовательно, соответствующий углу а поворота кривошипа угол 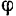 поворота линейки
поворота линейки 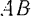 эллипсографа
эллипсографа
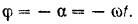
Таким образом, уравнениями движения линейки 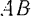 будут:
будут:
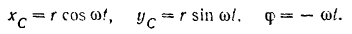
Координаты точки 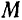 этой линейки в подвижной системе (рис. 144):
этой линейки в подвижной системе (рис. 144):
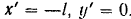
По формулам (99) находим теперь уравнения движения этой точки в плоскости 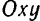 :
:
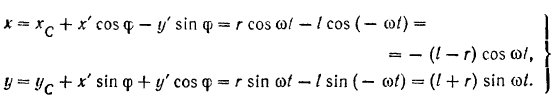
Полученные уравнения движения точки 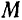 служат одновременно и уравнениями ее траектории в параметрической форме. Для того чтобы получить уравнение траектории в обычной форме, исключим из них параметр
служат одновременно и уравнениями ее траектории в параметрической форме. Для того чтобы получить уравнение траектории в обычной форме, исключим из них параметр 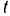 :
:
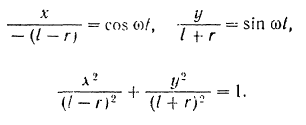
Следовательно, траекторией любой точки 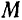 линейки будет эллипс с полуосями
линейки будет эллипс с полуосями
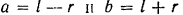
и центром в точке 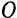 .
.
По найденным уравнениям (1) движения точки в прямоугольных координатах нетрудно найти как проекции
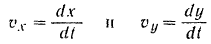
ее скорости, так и проекции
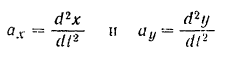
ее ускорения на координатные оси, а затем модули и направления скорости 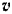 и ускорения
и ускорения 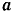 точки
точки 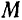 для любого момента времени.
для любого момента времени.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

