Оглавление:
Уравнения, допускающие понижение порядка
Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью замены переменной (подстановки) данное ДУ сводится к уравнению, порядок которого ниже.
Рассмотрим три типа уравнений, допускающих понижение порядка.
I. Пусть дано уравнение

Порядок можно понизить, введя новую функцию 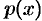 , положив
, положив 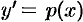 . Тогда
. Тогда 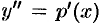 и получаем ДУ первого порядка:
и получаем ДУ первого порядка: 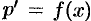 . Решив его, т. е. найдя функцию
. Решив его, т. е. найдя функцию 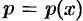 , решим уравнение
, решим уравнение 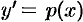 . Получим общее решение заданного уравнения (49.6).
. Получим общее решение заданного уравнения (49.6).
На практике поступают иначе: порядок понижается непосредственно путем последовательного интегрирования уравнения.
Так как 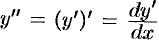 уравнение (49.6) можно записать в виде
уравнение (49.6) можно записать в виде 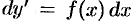 . Тогда, интегрируя уравнение
. Тогда, интегрируя уравнение 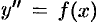 , получаем:
, получаем: 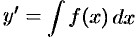 , или
, или 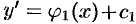 . Далее, интегрируя полученное уравнение по
. Далее, интегрируя полученное уравнение по  , находим:
, находим: 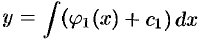 , т. е.
, т. е. 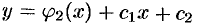 — общее решение данного уравнения.
— общее решение данного уравнения.
Если дано уравнение
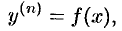
то, проинтегрировав его последовательно  раз, найдем общее решение уравнения:
раз, найдем общее решение уравнения: 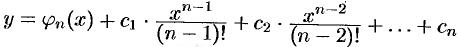 .
.
Пример №49.1.
Решить уравнение 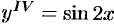 .
.
Решение: Последовательно интегрируя четыре раза данное уравнение, получим
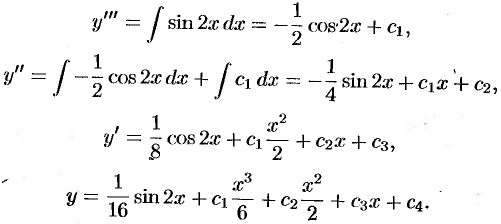
II. Пусть дано уравнение

не содержащее явно искомой функции  .
.
Обозначим 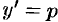 , где
, где 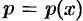 — новая неизвестная функция. Тогда
— новая неизвестная функция. Тогда 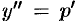 и уравнение (49.7) принимает вид
и уравнение (49.7) принимает вид 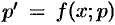 . Пусть
. Пусть 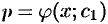 — общее решение полученного ДУ первого порядка. Заменяя функцию
— общее решение полученного ДУ первого порядка. Заменяя функцию 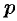 на
на 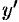 , получаем ДУ:
, получаем ДУ: 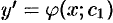 . Оно имеет вид (49.6). Для отыскания у достаточно проинтегрировать последнее уравнение. Общее решение уравнения (49.7) будет иметь вид
. Оно имеет вид (49.6). Для отыскания у достаточно проинтегрировать последнее уравнение. Общее решение уравнения (49.7) будет иметь вид 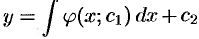 .
.
Частным случаем уравнения (49.7) является уравнение

не содержащее также и независимую переменную  . Оно интегрируется гем же способом:
. Оно интегрируется гем же способом: 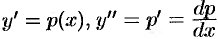 . Получаем уравнение
. Получаем уравнение 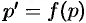 с разделяющимися переменными.
с разделяющимися переменными.
Если задано уравнение вида
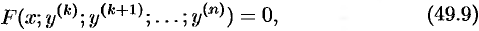
которое также не содержит явно искомой функции, то его порядок можно понизить на 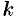 единиц, положив
единиц, положив 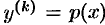 . Тогда
. Тогда 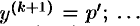 ;
; 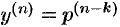 и уравнение (49.9) примет вид
и уравнение (49.9) примет вид 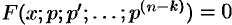 .
.
Частным случаем уравнения (49.9) является уравнение
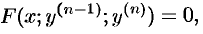
или
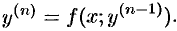
С помощью замены 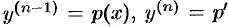 это уравнение сводится к ДУ первого порядка.
это уравнение сводится к ДУ первого порядка.
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Уравнение в полных дифференциалах интегрирующий множитель |
| Уравнения Лагранжа и Клеро |
| Линейные однородные ДУ второго порядка |
| Линейные однородные ДУ n-го порядка |

