Уравнение в полных дифференциалах. Интегрирующий множитель
Уравнение
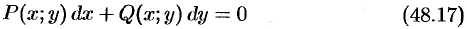
называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции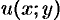 
, т. е.
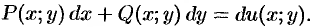
В этом случае ДУ (48.17) можно записать в виде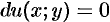 
, а его общий интеграл будет:
Приведем условие, по которому можно судить, что выражение
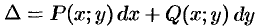
есть полный дифференциал.
Теорема 48.2. Для того чтобы выражение 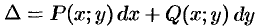, где функции 
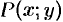и 
и 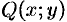их частные производные 
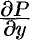и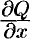 
непрерывны в некоторой области 
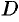плоскости 
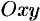, было полным дифференциалом, необходимо и достаточно выполнение условия
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Линейные уравнения Бернулли |
| Метод вариации произвольных постоянных |
| Уравнения Лагранжа и Клеро |
| Уравнения, допускающие понижение порядка |
