Оглавление:


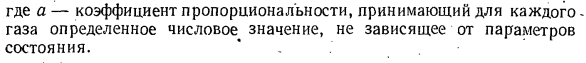


Уравнение состояния Ван-дер-Ваальса.
- Уравнение состояния ван-дер-Ваальса Сравнение состояний ван-дер-Ваальса является одной из первых попыток аналитического описания свойств экзистенциальных газов. 1 это уравнение ясно показывает качественные характеристики экзистенциальных газов. И; разница с идеалом. Как уже говорилось, реальный газ отличается от идеального наличием сил взаимодействия между молекулой
и объемом самой молекулы. Сила взаимодействия очень велика относительно твердого тела к жидкости, очень велика относительно газа, близка к переходу от газа к жидкости. 。 — от области перехода к жидкости, и чем больше расстояние между молекулами, тем меньше сила межмолекулярного взаимодействия, а состояние реального газа
Таким образом, чем дальше газовое состояние находится Людмила Фирмаль
ближе к идеальному. И наоборот, чем ближе состояние газа к жидкому режиму, тем больше сила взаимодействия и тем больше отклонение от характеристик идеального газа. Поэтому при изучении свойств реального газа необходимо учитывать силу взаимодействия между молекулой и объемом самой молекулы. Ван-дер-Ваальс ввел в уравнение 2 модификации, учитывающие отклонение реального
газа от идеального, для первого приближения. • Рассмотрим первую поправку, которая зависит от объема самой молекулы. Уравнение Клапейрона может быть выражено как в = RTfp. При увеличении давления объем v уменьшается, а для oo — » ■0.It идеально совпадает с определением идеального газа, в котором молекулы занимают бесконечно малые объемы. Учитывая реальный газ, который
- учитывает объем зазора между молекулами, когда молекулы занимают конечный объем, и когда молекулы полностью закупорены, свободный объем для молекулярного движения равен-b(b =измельчение+ изаз). значение b-это наименьший объем, который может сжимать газ. * В этих условиях уравнение Клапейрона
принимает иную форму. И-b = RT / p. — p и oo, то свободный объем v-b стремится к нулю или v-b. то есть при p oo объем газа становится величиной b, которая зависит от объема самой молекулы. Для каждого газа значение b принимает определенное число. Уравнение
Если полученная зависимость имеет тенденцию к увеличению давления Людмила Фирмаль
Клапейрона-идеальное давление газа, обусловленное、 Р = РТ / в、 А если фактический газ-учитывайте величину b: …….. Р = РТ /(в-б)、 При той же температуре, давление реального газа будет увеличиваться.」 •Это связано с тем, что фактический свободный объем газа меньше, чем идеальный газ, поэтому средний свободный путь молекул также меньше, поэтому фактические молекулы газа
сталкиваются со стенкой или»повышенным давлением». Во 2-й поправке, введенной в уравнение состояния, рассматривается влияние силы взаимодействия между молекулами. В идеальном газе отсутствует сила межмолекулярного взаимодействия, поэтому молекулы фактически свободны от движения, а воздействие на стенку сосуда никак не ограничено. —. В реальном Газе, когда
существует сила взаимодействия между молекулами, сила воздействия на стенку сосуда мала из-за того, что все молекулы на стенке сосуда притягиваются соседними молекулами в пространство. vessel. As в результате давление, прикладываемое реальным газом по сравнению с идеальным газом, уменьшается на величину Ap, которая является коррекцией давления*с учетом силы взаимодействия между молекулами. Эта поправка АП либо
прямо пропорциональна как числу притягиваемых молекул, так и числу притягиваемых молекул, либо прямо пропорциональна мощности 2 плотности газа, либо обратно пропорциональна мощности 2 его удельного объема. АП = ар2 = А / В2. 。 Где а-коэффициент пропорциональности и принимает конкретное число для каждого газа, независимо от параметра состояния. * Когда мы вводим 2-ю поправку、 RT: ЧТО ВЫ ДУМАЕТЕ? п — — — д-р или П В-Б
В-Б П2 Отсюда уравнение ван-дер-Ваальса-n•(p + aft? Он принимает форму (V-b)= RT. 。 (4-1) Это уравнение было опубликовано Ван дер Ваальсом в 1873 году. Величина a / v2 называется внутренним давлением: для жидкостей она принимает очень большое значение (293°K \ a (v и 10800 бар) для воды при температуре); для газов внутреннее давление относительно мало и зависит от давления
и температуры газов. Формула ван-дер-Ваальса правильно и качественно отражает поведение реальных веществ в жидком или газообразном состоянии state. In в случае двухфазного состояния это не применимо. Для газа в 1 кмоль формула Ван-дер-Ваальса записывается следующим образом: «(Р + я ^ з-з = Т 8314.2. Для реального газа, определяемого уравнением состояния Ван-Ваальса, главной частной производной параметра является u (h | th форма:. РТ 2а В П2 в $ ДТ \ в-б ДП)в р (в-Б) 2-У3 Р л• 2ab П〜
Смотрите также:
Решение задач по термодинамике
| Газовая постоянная смеси газов. | Анализ уравнения Ван-дер-Ваальса. |
| Свойства реальных газов. | Уравнение состояния для реальных газов М. П. Вукаловича и И. И. Новикова. |

