Уравнение состояния для реальных газов М. П. Вукаловича и И. И. Новикова.

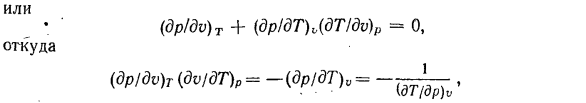
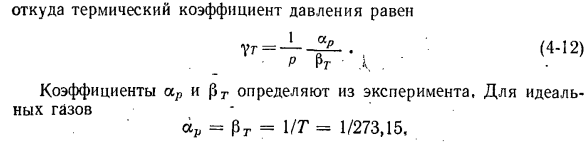
Уравнение состояния для реальных газов М. П. Вукаловича и И. И. Новикова.

• Уравнение состояния реального газа М. П. Вукалович и И. И. Новиков Уравнение ван-дер-Ваальса при больших плотностях газа дает некоторые дополнительные физические «явления», особенно так называемые силы, ассоциации и диссоциации молекул, дающие значительную ошибку из-за того, что вывод не был учтен. Кроме того, экспериментами было доказано, что коэффициенты а и 6,

содержащиеся в уравнении ван-дер-Ваальса, не могут быть постоянными величинами, но они должны зависеть от температуры и давления, и эта зависимость очень сложна. ван-дер-Ваальса путем введения дополнительных зависимостей с учетом изменчивости а и 6 существенно не расширили их область применения. Советский

Однако попытки многих ученых скорректировать уравнение Людмила Фирмаль

ученый М. П. Вукалович и И. И. Новиков предложили в 1939 году новое универсальное уравнение состояния экзистенциальных газов. Это качественно отличается от уравнения ван-дер-Ваальса. При выводе своих уравнений авторы учитывали указанное выше явление-объединение сил молекул под действием межмолекулярных

сил взаимодействия. Благодаря явлению ассоциации отдельные молекулы объединяются в группы, состоящие из 2,3,4 или более одиночных молекул. Отдельные молекулы, входящие в группу сложных частиц, не в полной мере реализуют все степени свободы, сохраняя при этом свои индивидуальные свойства. Таким образом,

• связывание молекул понимается как простая механическая связь 2, 3, 4 или более молекул с 1 сложной частицей, и в некоторых отношениях они ведут себя как независимые частицы газа. Ряд однородных газовых частиц образуется в результате объединения молекул. Но это считается обычным газом. Также рассмотрим собственно газ как смесь нескольких газов, частицами которых

являются одинарные, двойные, тройные и другие молекулярные группы. каждый из которых очень точно следует уравнению ван-дер-Ваальса. Закон массы применяется к таким газам, релевантность которых делится на группы по 2, 3 и 4 молекулы соответственно. П. Вукалович и И. И. Новиков получили уравнение состояния как основу для

Эти газы имеют определенное взаимодействие друг с другом Людмила Фирмаль

создания первой отечественной таблицы воды и водяного пара, которая была издана М. П. Вукаловичем в 1940 году. Позднее это уравнение было значительно уточнено, что значительно расширило границы его применения. application. In простейшая форма, Если рассматривать только двоичные комплексные числа, то уравнение

принимает вид: И 3 + 2t VT 2 Где w b-уравнение постоянной ВАП-дер-Ваальса. Решетка-постоянная, определяемая на основании экспериментальных данных* Частичная производная параметра состояния. Термический коэффициент Если уравнение состояния известно, то каждый параметр состояния может быть представлен

в виде функции от других 2 параметров. Р = фи(в, Р); Т = / 2(р, V); в = / 3(р, т). Полная дисперсия этих величин равна: {ДП / ДТ) в ДП =(dр / DV)Т ДВ-б ДТ、 ДТ =(ДТ / ДП) в ДП-Ф (ВШП / ДВ) ПДВ (4-7） (ДВ / ДТ) Р ДТ ДВ =(ДВ / с) п)т ДП-Ф Частные производные дифференциальных dp, dT, dv представляют собой пары значений,

противоположных друг другу, и в соответствии с правилами дифференциального исчисления между ними существуют следующие соотношения: (ДВ / ДП) Т(др / Ди)Т = 1; (ДТ / ДВ)п(ДВ / ДТ) Р = 1; (мощность) л(dTldp) с V = 1. Итак, 3 из них являются независимыми и частичными. В качестве этих независимых производных выбираются следующие: (ДП / ДТУ (dvldp) T и (ИДВ / ДТ) р. Эти частные

производные входят в Формулу тепловых коэффициентов (сжатия, расширения, термоупругости) и могут быть определены экспериментально. — Эти частные производные не являются независимыми. Каждый из них может быть представлен в виде 2 других функций. Уравнение dp =(dp / dv) Tdu +(другое!)ДТ) g4t компания P = рассматривается в const, а затем (ДП / ДВ) Тдвп +(ДП / ДТ)

тдтп = 0、 Или нему (DP / DV) Т +(dpldT) V(в dtlldv) р = » О、 Откуда нему (DP / DV)Т(ДВ / ДТ) Р—(ДП / ДТ) V в = (■ДТ / ДП) в 1 Или•• нему (DP / DV) Т (dTdT) п (ДТ / ДТ) 0 =-я (ОП / DV) Т 1 (4-8） 。Из последнего уравнения (dvldT) p (dT / dp) v =- Или (ду! д)М = — ^ / ДТ)<> (доктор! ДТ) о ’ Соотношение (4-8) позволяет установить зависимость между коэффициентом изотермического сжатия pb и коэффициентом

теплового расширения тела ap и коэффициентом теплового давления yt. «Эти величины, которые были измерены очень точно в экспериментах, важны для характеристики характеристик реального тела. Отношение частного дифференциала к объему V (dV / dp) t характеризует скорость изменения объема с увеличением давления при постоянной температуре. Это соотношение называется

коэффициентом сжатия объекта (4-9)） пт ^ — Ш (ду / др） Знак минус справа от равенства устанавливается следующим образом (dV / dp) T всегда отрицательное, поэтому оно оказывается положительным значением. Если давление остается постоянным, то отношение частного дифференциала (dV / dT) p к объему V характеризует

скорость изменения объема при нагревании. Это отношение называется коэффициентом теплового расширения тела V. АР = л / в(ДВ / ДТ) р. (4-10） Коэффициент в частных производных (dpldT) v и отношение давления p характеризуют интенсивность изменения давления с увеличением температуры, когда объем тела постоянен. Это отношение называется термическим модулем упругости, или

коэффициентом теплового давления (4-Р） В / = 1 / п (ДП / ДТ) в Подставляя значение частной производной в уравнение (4-8)、 Сияющий — Pt = — aP / YrP> , где коэффициент теплового давления равен Г(4-12） — Р Пр’л. Коэффициенты ar и rg определены из эксперимента с идеальным газом = Пр = УТ = 1 / 273.15、 Глава

IV вопросы безопасности 1.В чем разница между реальным и идеальным газом? 2.Что называется степенью сжатия? 3.Уравнение состояния реального газа с коэффициентом вириала. 4.Каково обоснование вывода уравнения ван-дер-Ваальса? 5. каково значение константы b в уравнении ван-дер-Ваальса? 6.Сколько стоит

внутреннее давление газа? 7. — Формула ван-дер-Ваальса для газа в l kg. 8.Рассмотрим уравнение ван-дер-Ваальса. 9.Ван-дер-Ваальс объясняет значение объемных корней при различных условиях вещества, полученных из уравнения. 10.Кто первым доказал существование важного момента? 11.Как вычисляются константы

a и b относительно критических параметров в уравнении ван-дер-Ваальса? 12.При каких условиях газ становится жидким? 13.Уравнение ван-дер-Ваальса для вышеуказанных параметров. 14.Законы каждого штата. 15 *.Что такое связывание молекулярных сил? 16. М. П. бы-калович и Я. что является основой для вывода уравнения состояния I / Novikov? 17.Какова изотермическая степень сжатия? 18.Каков коэффициент теплового расширения тела? 19.Что такое коэффициент теплового давления? 20.Как это связано с термическим коэффициентом?

Смотрите также:

Решение задач по термодинамике

Уравнение состояния Ван-дер-Ваальса.	Закон сохранения и превращения энергии.
Анализ уравнения Ван-дер-Ваальса.	Внутренняя энергия.