Уравнение прямой, проходящей через две точки
Пусть прямая проходит через точки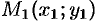 
и 
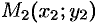. Уравнение прямой, проходящей через точку 
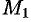, имеет вид
где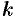 
— пока неизвестный коэффициент.
Так как прямая проходит через точку 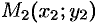, то координаты этой точки должны удовлетворять уравнению (10.6): 
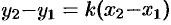. Отсюда находим 
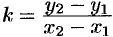. Подставляя найденное значение к в уравнение (10.6), получим уравнение прямой, проходящей через точк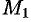и и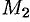 
:
Предполагается, что в этом уравнении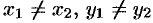 
.
Если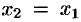 
, то прямая, проходящая через точк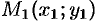и и 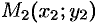, параллельна оси ординат. Ее уравнение имеет вид 
.
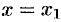Если 
, то уравнение прямой может быть записано в виде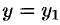 
, прямая 
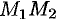параллельна оси абсцисс.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Поворот осей координат |
| Уравнение прямой, проходящей через данную точку в данном направлении |
| Уравнение прямой в отрезках |
| Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору |
