Уравнение прямой, проходящей через данную точку в данном направлении

Уравнение прямой, проходящей через данную точку в данном направлении

Пусть прямая проходит через точку 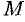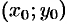и ее направление характеризуется угловым коэффициентом 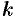. Уравнение этой прямой можно записать в ви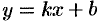де , где 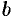— пока неизвестная величина. Так как прямая проходит через точку 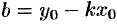, то координаты точки удовлетворяют уравнению прямой: 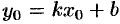. Отсюда 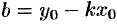. Подставляя значение 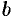в уравнение 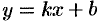, получим искомое уравнение прямой 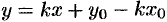, т. е.

Уравнение (10.5) с различными значениями 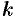называют также уравнениями пучка прямых, с центром в точке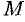 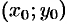. Из этого пучка нельзя определить лишь прямую, параллельную оси .

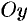На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Параллельный перенос осей координат

Поворот осей координат

Уравнение прямой, проходящей через две точки

Уравнение прямой в отрезках