Уравнение нервзрывности жидкости

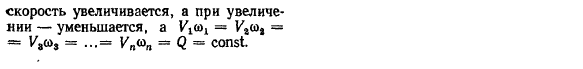
Уравнение нервзрывности жидкости

Уравнение нервзрывности жидкости. Уравнение неразрывности, или непрерывности жидкости, основано на законе сохранения массы, исходя из положения механики сплошной среды, в которой нет зазора внутри движущейся жидкости, а пустоты не могут быть установлены. Условия непрерывности могут быть выражены в дифференциальной форме для частиц жидкости и основных линий тока, а также в конечных величинах для потоков жидкости. В потоке выделите основной объем в виде параллелепипеда в виде ребристого круга, окружности, круга, круга (рис. 4.6). рассмотрим изменение массы жидкости, протекающей вдоль оси X.

Ими указывается скорость жидкости, текущей слева от параллелепипеда, а затем скорость жидкости, текущей с правой стороны、 может быть представлен в виде + * yh. Предполагая, что плотность жидкости p постоянна (см.§ 4.1), вы можете написать, что масса проходит через левую сторону в то же время. п ихуиуигш, справа от Р |них+ ых ^ yuigy1. −54. Разница в этих массах-P -^ r-yyyuyyy(. Аналогично, учитывая изменение массы жидкости вдоль оси y、 Р ~~ $ С ^ Г ^ hddgd! И-Р дддддуси. Закон сохранения массы требует, чтобы суммарное изменение массы, проходящее через выбранный объем, было равно нулю. -R ^ xuddgsK-r dhyugsiП dhuddgs = 0.

Так, в процессе движения жидкости должен выполняться закон сохранения массы. Математическим выражением этого закона в гидромеханике и служит уравнение неразрывности. Людмила Фирмаль

• Эта формула, в дифференциальной форме любого «движения несжимаемой жидкости», называется уравнением неразрывности или непрерывности. Левой частью уравнения(4.27) является относительная скорость изменения (объемного расширения) основного объема жидкости, называемая расхождением векторов скоростей (cNu и), то есть расхождением\ while <NUI =0.(4.28） Для стационарного движения уравнение неразрывности можно вывести из основных свойств струйки(см. 4.1).Согласно им, жидкость из потока не течет в сторону и не течет извне, но в то же время локальная скорость изменяется по длине потока.

• Таким образом, количество жидкости, вытекающей из струйки в первой живой секции, и количество жидкости, вытекающей из струйки в последней живой секции, равны, и общее количество жидкости в струе не изменяется. Рассмотрим элементарные потоки (рис.4.3) на участках 1-1 и 2-2 с локальными скоростями»x» и » иг » соответственно.Количество жидкости, прошедшее через Через разделы 1-1 и 2-2 в единицу времени они составляют базовую стоимость= u1d (o1 и= u2sc.Струйка cK} 1 = cK} 2 по величине инварианта у ^ уй = у ^ г CO2 (4.29).

Мы математически выражаем закон сохранения массы, открытый М. В. Ломоносовым. Людмила Фирмаль

• Формула (4.29)представляет собой уравнение непрерывности или непрерывности основного потока. В соответствии с зависимым потоком (4.11), для ряда основных потоков, потока жидкости (рис.4.4), можно записать@ 1 = ^ 1<sup class=»reg»>®</sup>1 и φ2= P2co2. 1> x = P2CO2. (4.30)） Эта формула представляет собой уравнение непрерывности или непрерывности потока жидкости, где p = const! Выражение (4.30) может быть выражено следующим образом То есть отношение средней скорости живого сечения потока обратно пропорционально отношению его площади. 55. Из уравнений(4.30) и (4.31) следует, что стационарное движение жидкости сопровождается важными особенностями.

Смотрите также:

Задачи по гидравлике

Возможно эти страницы вам будут полезны:

1. Поток жидкости и его элементы.
2. Дифференциальные уравнения движения невязкой жидкости (уравнения Эйлера)
3. Особенности потенциального движения жидкости.
4. Примеры плоских потенциальных движений жидкости